分布參數系統辨識

根據實驗數據來估計分布參數系統數學模型中的未知參數（常數或函式）、未知邊值條件或未知邊界形狀的系統辨識方法。

正文

系統參數辨識

分布參數系統的數學模型由如下的狀態方程、邊界條件和初始條件組成：
狀態方程：e(u(x，t),x，t，a)＝0 x∈Ω t∈【0,T】
邊界條件:b(u(x，t),x，t，a)＝0　x∈坸Ω t∈【0,T】
初始條件：c(u(x,0))＝C0(x)x∈Ω
式中Ω是系統的空間區域；坸Ω表示空間區域Ω的邊界；【0,T】表示從零時刻到T時刻的時間區間；∈為屬於符號，a是未知參數。未知參數a被限制在允許的未知參數集A中。輸出方程是:z＝Cu(x，t，a),式中C為觀測運算元。此類辨識問題就是根據觀測值z來估計未知參數a。為了評價參數估計的好壞，選擇一個性能指標J(a)，於是分布參數系統的辨識問題就變為最佳化問題，即求╋∈A，使

式中╋就是所要求的估計參數。輸出誤差的平方常被用來作性能指標，即

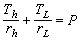
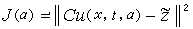
式中╋為實際測量到的輸出，Cu(x，t，a)為根據模型算出的輸出，‖·‖為在觀測空間中的範數。選擇姙作為模型的參數就意味著該模型最接近真實系統，因而也就完成了對模型參數a的辨識。

根據未知參數所處地位的不同，分布參數系統辨識又可分為：①未知係數的辨識，指未知參數含在狀態方程的係數中；②未知邊值條件的辨識，指未知參數含在邊值條件中；③未知邊界形狀的辨識，指未知參數為描寫邊界形狀的幾何變數，此時的最佳化問題又稱為最優設計問題；④未知初值條件的辨識，指未知參數為初始狀態，此類辨識一般稱為狀態估計問題。

分布參數系統辨識的算法大體上可分為兩類。一類是直接對分布參數模型（狀態空間為無窮維）用最佳化方法。另一類是首先用集中參數系統模型近似地表示分布參數系統模型，然後用集中參數系統辨識的算法來求解。

在用最佳化方法求解分布參數系統的辨識問題時，如果最佳化問題存在解，且此解具有唯一性，並對觀測數據具有連續的依賴性，則稱該系統是可辨識的。這種性質就稱為可辨識性。