定義
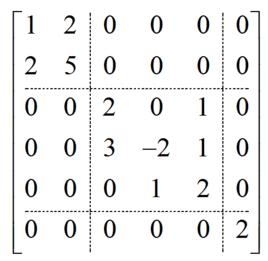
將一個矩陣用若干條橫線和豎線分成許多個小矩陣,將每個小矩陣稱為這個矩陣的子塊,以子塊為元素的形式上的矩陣稱為分塊矩陣。
例如,
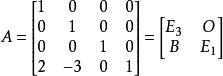 分塊矩陣
分塊矩陣 分塊矩陣
分塊矩陣其中 E, E分別表示1階、3階單位矩陣, O表示3×1零矩陣,而 。
同一個矩陣可以有多種不同的分塊方法,從而形成不同的分塊矩陣。例如上例的矩陣也可分成也可分成
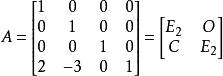 分塊矩陣
分塊矩陣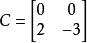 分塊矩陣
分塊矩陣其中 E表示2階單位矩陣, O表示2階零矩陣,而 。
運算規則
加法
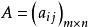 分塊矩陣
分塊矩陣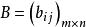 分塊矩陣
分塊矩陣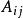 分塊矩陣
分塊矩陣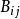 分塊矩陣
分塊矩陣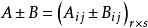 分塊矩陣
分塊矩陣設 , ,用同樣的方法對 A, B進行分塊,即 , 為同型矩陣,則 。
數乘
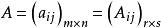 分塊矩陣
分塊矩陣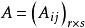 分塊矩陣
分塊矩陣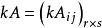 分塊矩陣
分塊矩陣設 , k是任意數,定義分塊矩陣 與 k的數乘為 。
乘法
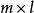 分塊矩陣
分塊矩陣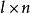 分塊矩陣
分塊矩陣 分塊矩陣
分塊矩陣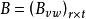 分塊矩陣
分塊矩陣設 A是 階矩陣,B是 階矩陣,即A的列數=B的行數,分塊 , ,即A的列分塊法=B的行分塊法。
 分塊矩陣
分塊矩陣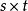 分塊矩陣
分塊矩陣則A與B的乘積 是 階分塊矩陣,
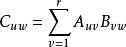 分塊矩陣
分塊矩陣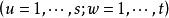 分塊矩陣
分塊矩陣其中, 。
轉置
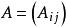 分塊矩陣
分塊矩陣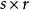 分塊矩陣
分塊矩陣 分塊矩陣
分塊矩陣 分塊矩陣
分塊矩陣設矩陣 是 階分塊矩陣, ,則 。
特殊分塊矩陣
分塊對角矩陣
設 A為 n階方陣,若 A的分塊矩陣在非主對角線上的子塊皆為零矩陣,且在主對角線上的子塊都是方陣,即
 分塊矩陣
分塊矩陣 分塊矩陣
分塊矩陣其中 O表示零矩陣, 都是方陣,那么稱 A為分塊對角矩陣。
性質:
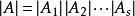 分塊矩陣
分塊矩陣① ;
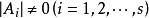 分塊矩陣
分塊矩陣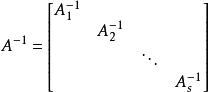 分塊矩陣
分塊矩陣②若 ,則 A可逆,且 ;
③同結構的準對角矩陣的和、差、積、數乘及逆仍是準對角矩陣,且運算表現為對應子塊的運算。
分塊上下三角矩陣
對方陣進行分塊後,主對角線上的子塊矩陣都是方陣,主對角線以下(以上)的子塊矩陣都是零矩陣,即
 分塊矩陣
分塊矩陣或
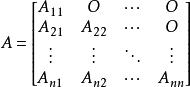 分塊矩陣
分塊矩陣稱為分塊上(下)三角形矩陣。
性質 :
①同結構的分塊上(下)三角形矩陣的和(差)、積(若乘法運算能進行)仍是同結構的分塊矩陣。
② 數乘分塊上(下)三角形矩陣也是分塊上(下)三角形矩陣。
③ 分塊上(下)三角形矩陣可逆的充分必要條件是的主對角線子塊都可逆;若可逆,則的逆陣也是分塊上(下)三角形矩陣。
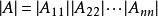 分塊矩陣
分塊矩陣④ 分塊上(下)三角形矩陣對應的行列式:。