共邊定理

有一條公共邊的三角形叫做共邊三角形。
幾何課本里有相似三角形、全等三角形，但沒有共邊三角形。其實，共邊三角形在幾何圖形中出現的頻率更多。比如，平面上隨意取四個點A、B、C、D，這其中一般沒有相似三角形，也沒有全等三角形，但卻有許多共邊三角形。由此，我們說一下共邊定理
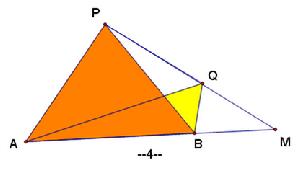
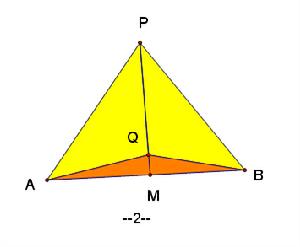
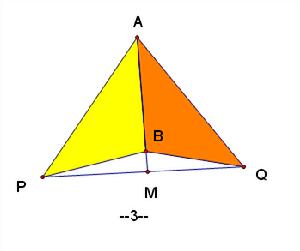
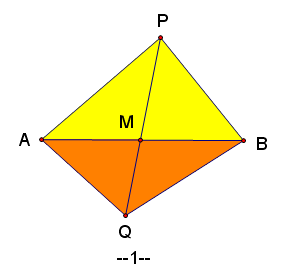
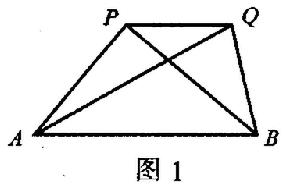
共邊定理：設直線AB與PQ交於點M，則S△PAB/S△QAB=PM/QM
證明：分如下四種情況，分別作三角形高，由相似三角形可證
證法2：△PAB\△QAB=△PAB\△PMB×△QMB\△QAB=AB\MB×PM\QM=PM\QM

特殊情況：當PQ∥AB時，易知△PAB與△QAB的高相等，從而S△PAB=S△QAB，反之，S△PAB=△QAB，則PQ∥AB