簡介
共軛線性運算元是由線性運算元誘導出的共軛空間之間的運算元。
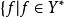共軛線性運算元設X,Y為賦范線性空間，T是X到Y的稠定線性運算元。記* =，存在g∈X*，使對一切x∈(T)，g(x)=f(Tx)成立}，這裡g由f惟一確定，*是Y*的線性子空間，在D*上定義運算元T*:T*f=g，T*是以*為定義域的到X*的線性運算元，並稱為T的共軛運算元，也稱為T的對偶線性運算元或伴隨線性運算元。
性質
當T是有界線性運算元時，T*也是有界的，並且‖T*‖= ‖T‖。有界線性運算元的共軛運算元有如下基本性質：
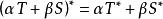共軛線性運算元（a,β 是數）；
(TS)* = S*T*；
(T )* = (T*) 。
套用
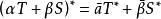共軛線性運算元當X,Y是內積空間時，T的共軛運算元T*是指滿足(Tx,y)=(x,T*y)的線性運算元。內積空間的共軛運算元是線性代數中轉置共軛矩陣概念的推廣，它與賦范空間上共軛運算元的性質的區別僅在於（α,β是數）。特別地，當X=Y是希爾伯特空間時有：
1.若A∈(X),則A*∈(X)；
2.A**=A；
3.‖A*A‖= ‖A‖ ；
4.ker(A)=(A*) ，ker(A*)= :(A) ，這裡的ker(A)為運算元A的零空間。
賦范空間中共軛運算元是線性代數中轉置矩陣概念的推廣，所以自然地在研究方程Tx=y時它起著重要作用。
