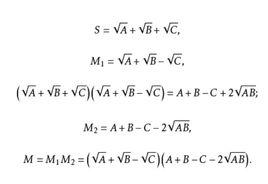基本介紹
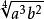 共軛因式
共軛因式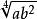 共軛因式
共軛因式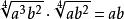 共軛因式
共軛因式共軛因式亦稱有理化因式、有理化因子,指乘積為有理式的兩個無理式。若兩個含有根式的代數式S與M的乘積SM是有理式,則它們互稱共軛因式。例如,式子 (a>0,b>0)的共軛因式是 ,因為 。一個式子的共軛因式乘以一個有理式仍是這個式子的共軛因式,所以,一個式子的共軛因式不是惟一的 。
求共軛因式的方法
常用的求共軛因式的方法如下 :
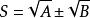 共軛因式
共軛因式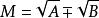 共軛因式
共軛因式1.對於 ,可取 作為共軛因式。
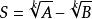 共軛因式
共軛因式2.對於 ,可取
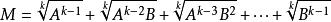 共軛因式
共軛因式作為共軛因式。
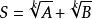 共軛因式
共軛因式3.對於 ,可取
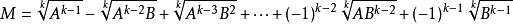 共軛因式
共軛因式作為共軛因式。
4.有時對共軛因式的尋求要逐步完成 。
例如對於
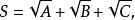 共軛因式
共軛因式則應取
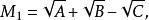 共軛因式
共軛因式可得
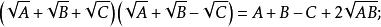 共軛因式
共軛因式可再取
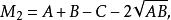 共軛因式
共軛因式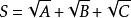 共軛因式
共軛因式於是 的共軛因式為
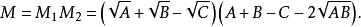 共軛因式
共軛因式5.待定係數法。
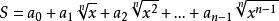 共軛因式
共軛因式例如,求 的共軛因式,可取
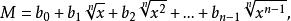 共軛因式
共軛因式係數b(i=0,1,2,…,n-1)由S·M為有理式這一條件確定。
6.對於給定的含有根式的代數式,如果可以看成是某一根式的多項式P(x),則可利用互質多項式P(x)和Q(x)的性質,輾轉相除,可得多項式M(x)與N(x),使得M(x)P(x)+N(x)Q(x)=1,則M(x)即為P(x)的共軛因式。
7.對於表達式
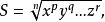 共軛因式
共軛因式(此處p, q, …, r是小於n的自然數), 可取
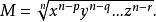 共軛因式
共軛因式求共軛因式常用於根式運算的使分母(或分子)有理化的過程中。中國的《九章算術》“少廣”章中敘述有:“若母不可開者,又以母乘定實,乃開之,訖,令如母而一。”譯為現代算術,即
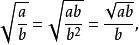 共軛因式
共軛因式足見其已有了有理化分母的思想,秦九韶在所著《數書九章》中,也運用了有理化方法 。