基本介紹
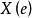共軛反對稱函式
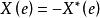共軛反對稱函式 共軛反對稱函式共軛反對稱函式(conjugate antisymmetric function)是指具有共軛反對稱特性的一種頻譜函式，序列的傅立葉變換，通常稱為序列的頻譜函式，如果頻譜函式滿足，則稱為 共軛反對稱函式，式中符號*表示複數共軛，奇序列的傅立葉變換，均為共軛反對稱函式 。
詳細介紹
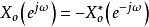共軛反對稱函式
共軛反對稱函式 共軛反對稱函式滿足的函式稱為 共軛反對稱函式。可以將寫成
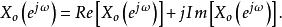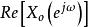共軛反對稱函式 共軛反對稱函式
共軛反對稱函式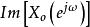
共軛反對稱函式
共軛反對稱函式 共軛反對稱函式不難證明：共軛反對稱函式的實部是的奇函式，虛部是的偶函式。
共軛反對稱函式 共軛反對稱函式傅立葉變換作為的連續函式可以分解成共軛對稱與共軛反對稱函式之和，即
共軛反對稱函式式中
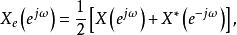共軛反對稱函式且
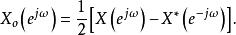共軛反對稱函式
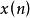共軛反對稱函式 共軛反對稱函式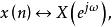
共軛反對稱函式如果將復序列的及其傅立葉變換之間的關係記為：則可以證明
(1)
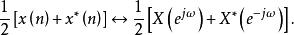共軛反對稱函式 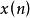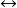共軛反對稱函式
共軛反對稱函式 共軛反對稱函式(的實部的共軛對稱分量)
(2)
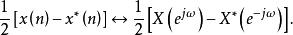共軛反對稱函式 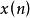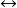共軛反對稱函式 共軛反對稱函式 共軛反對稱函式(的虛部的共軛反對稱分量)
(3)
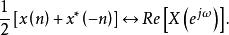共軛反對稱函式 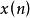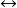共軛反對稱函式 共軛反對稱函式 共軛反對稱函式(的共軛對稱分量的實部)
(4)
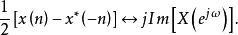共軛反對稱函式 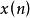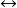共軛反對稱函式 共軛反對稱函式 共軛反對稱函式(的共軛反對稱分量的虛部)
注意： (1)和(3) 以及(2) 和(4)的 對偶性質。
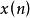共軛反對稱函式如果是實序列，則上述對稱性變得特別簡單和有用。
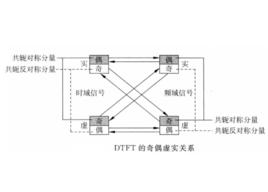
時域、頻域序列都有實部和虛部，而它們又各有偶對稱和奇對稱分量，容易證明，各個分量之間的變換關係如圖1所示。圖中標出了時域、頻域的共軛對稱與共軛反對稱分量 。
舉例說明
【 例1】 證明：若時域序列只有實部，它的傅立葉變換的實部是偶函式，虛部則是奇函式。
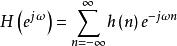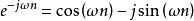共軛反對稱函式 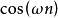共軛反對稱函式
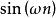共軛反對稱函式
共軛反對稱函式
共軛反對稱函式
共軛反對稱函式
共軛反對稱函式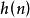
共軛反對稱函式
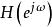共軛反對稱函式解： 在正變換式中，等式左邊是的函式。右邊對變數n求和。復指數序列可寫成。其中，和分別是n的偶函式(記為)和奇函式(記為)。包含偶部he和奇部ho。由實部Hr和虛部Hi組成。所以，正變換式可表示為
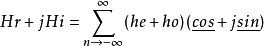共軛反對稱函式
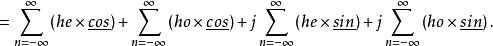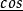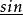共軛反對稱函式
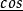共軛反對稱函式
共軛反對稱函式 共軛反對稱函式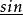 共軛反對稱函式 共軛反對稱函式 共軛反對稱函式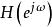 共軛反對稱函式上式右邊對n求和。由於he和是n的偶函式，而ho和是n的奇函式，所以求和後，第2項和第3項為0，而剩下第1項和第3項。第1項的是的偶函式，第4項的是的奇函式。由此可見，的實部是偶函式，虛部是奇函式 。
【 例2】證明時域的共軛對稱分量由實部的偶分量和虛部的奇分量組成，即
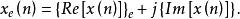共軛反對稱函式(下標“e”表示偶分量，“o”表示奇分量)
並說明時域的共軛對稱分量的傅立葉變換隻有實部。
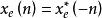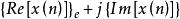共軛反對稱函式
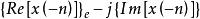共軛反對稱函式
共軛反對稱函式
共軛反對稱函式解：共軛對稱分量的定義是。先使的變數n改為一n，得。然後取共軛，得。於是本題得證。根據DTFT的奇偶虛實關係，時域的共軛對稱分量的傅立葉變換隻有實部 。
