概念
1932年，Wigner在量子力學中引進了時間反演，乍一看來，這是與空間反演相似的一個分立對稱性，實際上不然。這是用詞不當。嚴格地說，所謂的時間反演對稱乃是指運動的可逆性，即把一個過程用攝像機拍下來，然後把膠捲倒過來放映，假如看上去運動規律（當然不是指“現象”）與順放時一樣，就叫做“時間反演守恆”。
基本原理
對一個無自旋粒子在位形空間寫出薛丁格方程：
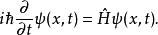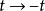時間反演算符
時間反演算符
時間反演算符 時間反演算符按上述定義，讓我們先作變換 ，看變換後對 的薛丁格方程是否能保持與原來有同樣形式？顯然不能！這時因為方程對 的微商是一階而非二階的緣故。於是在第二步，對整個方程取一次復共軛運算，才能得到預期的“時間反演不變的”薛丁格方程。
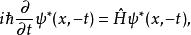時間反演算符
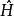時間反演算符
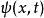時間反演算符
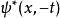時間反演算符其中已假設 不含時間，於是原來的 與 這兩個解之間有某種對稱性或等價性的關係。這是可能的，試看一個定態波函式，我們有：
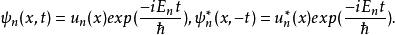時間反演算符於是有兩種可能性：
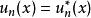時間反演算符
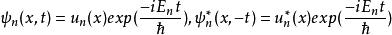時間反演算符 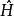時間反演算符
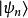時間反演算符
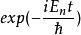時間反演算符（1） 是實函式， 的兩個態是同一個態。即當 在時間反演下不變且本徵態（在能量上）非簡併時，其相應之本徵波函式必可寫成（實函式）的形式。
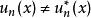時間反演算符 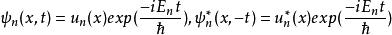時間反演算符
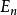時間反演算符
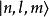時間反演算符
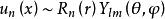時間反演算符
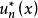時間反演算符
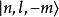時間反演算符
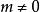時間反演算符
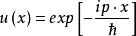時間反演算符
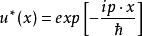時間反演算符（2），的兩個態不同，但有同樣的能量，所以是簡併態。例如在中心勢場中的能量本徵態，，而對應於，當時，它們是簡併的，且互為“時間反演態”。另一粒子是平面波，此時，它與在能量上簡併。
