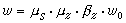公式推演
正文
由計算機自動推演數學公式的技術，是人工智慧的一個套用領域，又稱計算機代數。運用公式推演技術能使人們從手工的繁瑣和容易出錯的符號演算和推理中擺脫出來。(3+4)2=49,這是數值計算;而(a+b)2=a2+2ab+b2就是公式推演，這時被計算對象是符號式，結果也是符號式。公式推演的研究始於1953年。1966年美國計算機協會成立符號和代數推演專業組(SIGSAM)，並出版了這方面的刊物《ACM SIGSAM Bulletin》。
公式推演的內容包括數學式的化簡、多項式四則運算、求最大公因式、因式分解、有理式的各種運算、符號矩陣、行列式、張量運算、線性和非線性方程組的符號解、符號微分、不定積分、常微分方程和數理方程的解析解、各種特殊函式的推導和函式的級數展開等。公式推演的研究分為算法、系統和套用三個方面。
算法 針對各種公式推演對象，改進已有算法或提出新算法。例如求兩個多項式的最大公因式的算法、因式分解算法、求有理函式的不定積分的算法等。
系統 目前世界上已有60多個公式推演系統，可分通用系統和專用系統兩種類型。如美國麻省理工學院研製的MACSYMA,是著名的通用公式推演系統，也是求解數學問題的大型知識型系統或專家系統；ASHMEDAI則是量子電動力學問題的專用公式推演系統。muMATH是適於在微型機上運行的公式推演系統。
MACSYMA是互動式電腦程式系統,它以符號形式輸入和輸出，並可調用多種數值計算的子程式庫和繪圖程式包,因此公式推演功能很強。這個系統已與美國高級研究計畫局的通信網路即阿帕網(ARPA網)聯網。MACSYMA的化簡程式能自動地根據一組規則對數學式進行化簡，這類規則的例子如
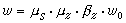
表達式尺寸大小(即所含項數多少)是衡量表達式簡單程度的一個有用指標。根據最小表達式的思想，MAC-SYMA採用了一個面向搜尋的爬山程式（算法），它對數學表達式的化簡如下例：
已知條件： K2+L2=1
N2-M2=1
原始表達式： K2N2+K2M2N2-K2L2N2-K2L2M2N2
中間表達式： K4M2N2+K4N2（原始式代換L而得）
最終表達式： K4N4（中間式代換M而得）
在某些問題中為便於化簡，數學式中的符號在取值範圍或其他性質方面受到一定限制,為此MACSYMA設定了一個關係資料庫，以語義網路形式存放關於符號的事實。例如用戶通過說明命令規定符號 m的值限為整數，那么化簡程式能將
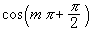簡化為零。又如用戶通過假設命令設定x ≤y，y≤z和z ≤x，那么MACSYMA便能推出x=y=z。 MACSYMA有一個自動符號積分程式,它使用啟發式技術。積分程式將被積函式分為11類，相應就有11個積分功能模組。積分程式根據被積函式中子式的啟示，將它交給相應的積分功能塊去處理。例如被積函式含有子式sin(2x),則用三角函式的積分功能塊去處理。遇到積不出的情況，符號積分程式會給出報告。
為了便利用戶,MACSYMA提供了在線上支援程式和用戶培訓程式（智慧型化計算機輔助數學程式）。
套用 公式推演技術已成功地用於天體力學、相對論、高能物理、電漿物理、量子電動力學、流體力學、數學、化學、電路網路理論、排隊論等科學領域,也成功地用於船體設計、直升機設計、電子顯微鏡設計等工程技術問題。MACSYMA系統已移交美國的能源研究與開發局、國家航空航天局、全國衛生研究院和海軍實驗室使用。
在求解一組描述天體運動規律（包括行星、人造衛星、太空站等）的微分方程時，通常採用逐次逼近法。解的形式是以小參數（如軌道的偏心率）表示的冪級數。從1847年起法國天文學家 G.-E.德洛內為研究月球運動公式花了20年時間，而1970年美國西雅圖波音實驗室的A.德普瑞特等人用公式推演和數值計算相結合的技術在計算機上只用了20小時就重新算出德洛內的公式並糾正了三處錯誤。
R.P.費因曼用他建立的費因曼圖來研究量子電動力學中電子和光子間相互作用的微擾理論。對電子異常磁矩進行準確到六階微量的修正計算，需要分析72張費因曼圖，涉及大量繁瑣的積分運算。套用公式推演技術可將積分結果先用符號形式表示, 然後再進行數值計算， 能大大提高計算效率。在 UNIVAC1108 機上運行專用的ASHMEDAI系統對一張複雜的費因曼圖進行分析僅需要35分鐘。
