全連續映射

全連續映射是映有界集為相對緊集的連續映射，緊連續映射必為全連續映射。

簡介

全連續映射是映有界集為相對緊集的連續映射。

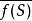全連續映射

設Ω⊂X，f:Ω→Y是連續映射。若對於Ω中的任何有界子集S，是Y中的緊集，則稱f為全連續映射。

性質

緊連續映射必為全連續映射。當Ω為有界集時，Ω上的全連續映射與緊連續映射是等價的概念。

設Ω為X中的有界集，則f:Ω→Y為全連續映射的充分必要條件是：f能用Ω上的有限維值連續映射一致逼近。

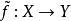全連續映射

可微的全連續映射在每點的導運算元是全連續線性運算元。設D為X中的有界閉集，f:D→Y全連續，則存在f在X上的全連續延拓，使得

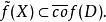全連續映射

連續映射

(continuous mapping)

連續映射拓撲空間之間的一類重要映射。

設(X,T)與(Y,Τ)是兩個拓撲空間，f:X→Y是映射，x∈X。若f(x)的每一鄰域關於f的原像是x的鄰域，則稱f在點x處是連續的。若f在X的任意點是連續的，則稱f是(X,T)到(Y,U)的連續映射。