多面體的內切球
如果一個球與簡單多面體的各面或其延展部分都相切,且此球在多面體的內部,則稱這個球為此多面體的內切球(inscribed sphere of a polyhedron)。多面體稱為這個球的外切多面體,正多面體的內切球均存在,正多面體內任意點到各面距離之和為常數
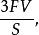 內切球
內切球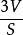 內切球
內切球這裡F為多面體的面數,S為表面積,V為體積,故正多面體內切球半徑為。
圓柱的內切球
與圓柱兩底面以及每條母線都相切的球稱為這個圓柱的內切球(inscribed sphere in a circular cylinder),此圓柱稱為球的外切圓柱,等邊圓柱才有內切球,球心在圓柱軸線中點處,內切球半徑與圓柱底面圓半徑相等。
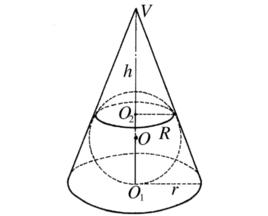
圓錐的內切球
與圓錐的底面和各母線均相切的球,稱為圓錐的內切球(inscribed sphere in a circular cone),此圓錐稱為球的外切圓錐。圓錐的內切球有且僅有一個,球心在圓錐的軸線上,當圓錐高為h,底面圓半徑為r時,則內切球半徑
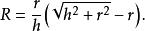 內切球
內切球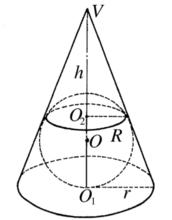 圖1
圖1圓台的內切球
與圓台的上、下底面以及每條母線都相切的球,稱為圓台的內切球(inscribed sphere in a frustum of a circular cone),此圓台稱為球的外切圓台,若且唯若母線長與上、下兩底面圓半徑之和相等時,圓台才有內切球 。