基本簡介
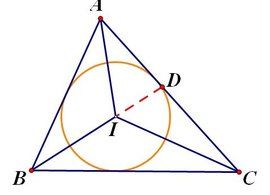
在數學中,若一個二維平面上的多邊形的每條邊都能與多邊形內部的一個圓形相切,該圓就是多邊形的內切圓,這時稱這個多邊形為圓外切多邊形。它亦是多邊形內部最大的圓形。內切圓的圓心被稱為該多邊形的內心。一個多邊形至多有一個內切圓,也就是說對於一個多邊形,它的內切圓,如果存在的話,是唯一的。並非所有的多邊形都有內切圓。三角形和正多邊形一定有內切圓。擁有外接圓的四邊形被稱為圓外切四邊形。
計算
1)對於一般的三角形,內切圓半徑公式如下:
r=sqrt[(p-a)(p-b)(p-c)/p]【sqrt為開平方根(square root)】
2)在直角三角形的內切圓中,有這樣兩個簡便公式:
1、兩直角邊相加的和減去斜邊後除以2,得數是內切圓的半徑:
r=(a+b-c)/2(註:s是Rt△的面積,a, b是Rt△的2個直角邊,c是斜邊)
2、兩直角邊乘積除以直角三角形周長,得數是內切圓的半徑:
r=ab/ (a+b+c)
補充
扇形內切圓
與扇形⌒AOB的圓弧⌒AB及兩條半徑OA,OB都相切的圓叫扇形的內切圓 .
內切圓圓心O′在扇形的圓心角AOB的角平分線上,
OO′=R-r(R是扇形半徑,r是內切圓半徑)
過O′作O′A⊥OA,垂足A,直角三角形OAO′中
∠O′OA=30°,O′A=r,OO′=R-r,
∴r=(R-r)*sin30°,r=1/2(R-r),R=3r
內切圓面積=πr^2,
扇形面積是原來圓面積的60/360=1/6
∴扇形面積=πR^2/6=π(3r)^2/6=3πr^2/2
∴扇形的內切圓面積與扇形面積的比為πr^2:(3πr^2/2)=2:3
直角三角形的內切圓的半徑=二分之一×(直角邊+另一直角邊-斜邊)
內切圓的半徑為r=2S÷C,當中S表示三角形的面積,C表示三角形的周長。
內切圓等於外切圓的2分之1
面積與原正方形比為π:4