基本介紹
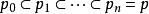 克魯爾維數
克魯爾維數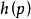 克魯爾維數
克魯爾維數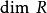 克魯爾維數
克魯爾維數 克魯爾維數
克魯爾維數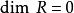 克魯爾維數
克魯爾維數克魯爾維數(Krull dimension)是決定環結構的一個參數,對賦值環的研究有重要意義。設p是R的素理想,R中終止於p的素理想真升鏈的長度n的最大值稱為素理想p的高,記為,R的理想a的高是包含在a中的所有素理想真升鏈的最大長度,環的克魯爾維數是指R中素理想真升鏈長度的最大值,記為。它是一個非負整數或。例如,域的維數為零,整數環的維數為1,一般地,環R為阿廷環若且唯若R為諾特環且。
相關介紹
在代數幾何史上,維數的定義經歷了三個階段:最早是按流形的定義,即局部解析同構於n 維單位球的流形為n 維;到上個世紀末,德國學派將代數集的維數定義為函式域(在常數域上) 的超越次數;而本世紀40 年代至今採用克魯爾維數,即函式環中素理想列的最大長度,每個新定義都和原來的一致,但適用範圍更廣。
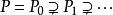 克魯爾維數
克魯爾維數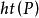 克魯爾維數
克魯爾維數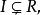 克魯爾維數
克魯爾維數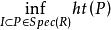 克魯爾維數
克魯爾維數 克魯爾維數
克魯爾維數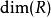 克魯爾維數
克魯爾維數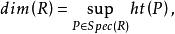 克魯爾維數
克魯爾維數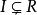 克魯爾維數
克魯爾維數定義設P是環R的素理想,則素理想列的長度的上界稱為P的高度,記為。對任一理想稱為的高度。R中素理想列的長度的上界稱為R的 克魯爾維數(簡稱 維數),記為。顯然且對任一理想有
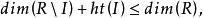 克魯爾維數
克魯爾維數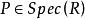 克魯爾維數
克魯爾維數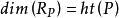 克魯爾維數
克魯爾維數對任意有。
例: 阿廷環就是0 維諾特環;戴德金環就是1維整閉諾特整環。
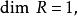 克魯爾維數
克魯爾維數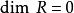 克魯爾維數
克魯爾維數如果R是戴得金環,則這是因為每個非零素理想都是極大理想。如果R是整環,則若且唯若R是域,下一命題刻畫了克魯爾維數為0的諾特環。
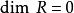 克魯爾維數
克魯爾維數命題如果R是諾特環,則若且唯若每個有限生成R-模M都有合成列 。

