定義
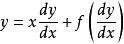 克萊羅方程
克萊羅方程形如 的方程,稱為克萊羅微分方程,這裡 f 是連續可微函式。
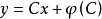 克萊羅方程
克萊羅方程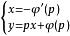 克萊羅方程
克萊羅方程克萊羅方程的通解具有形式:(直線族),此外存在奇解(包絡),其中奇解可以通過方程組:消去參數 p 而得到。
方程求解
方程的通解
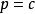 克萊羅方程
克萊羅方程克萊羅方程的通解可以通過令(任意常數),代入原方程中求得。
具體求解步驟
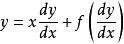 克萊羅方程
克萊羅方程已知方程:,
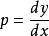 克萊羅方程
克萊羅方程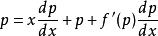 克萊羅方程
克萊羅方程對上式左右兩端同時對 x 求導,並令,可得:;
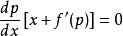 克萊羅方程
克萊羅方程即有:。
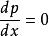 克萊羅方程
克萊羅方程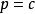 克萊羅方程
克萊羅方程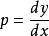 克萊羅方程
克萊羅方程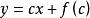 克萊羅方程
克萊羅方程(1)如果,則得到,將其代入到式子中可得:,其中 c 為任意常數,這就是原方程的解。
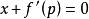 克萊羅方程
克萊羅方程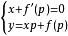 克萊羅方程
克萊羅方程(2)如果 ,則將該式與原方程聯立,得到方程組: ,消去 p 則得到方程的一個解。求此解的過程與求包絡的過程是一致的。不難驗證,此解正是通解的包絡。由此,克萊羅微分方程的通解為一直線族,即在原方程中以 c 代 p,且此直線族的包絡是方程的奇解。
典例
例1
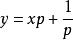 克萊羅方程
克萊羅方程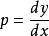 克萊羅方程
克萊羅方程求解方程 ,其中 。
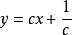 克萊羅方程
克萊羅方程解:這是克萊羅方程,因而易得其通解為,
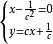 克萊羅方程
克萊羅方程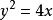 克萊羅方程
克萊羅方程從方程組 中消去 c,得到奇解:。
方程的通解是直線族,而奇解是通解的包絡。
例2
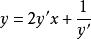 克萊羅方程
克萊羅方程解方程 。
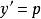 克萊羅方程
克萊羅方程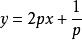 克萊羅方程
克萊羅方程解:令 ,則有。
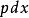 克萊羅方程
克萊羅方程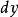 克萊羅方程
克萊羅方程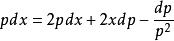 克萊羅方程
克萊羅方程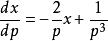 克萊羅方程
克萊羅方程微分後,以代替,我們得到:或者。
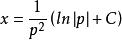 克萊羅方程
克萊羅方程求解這個線性方程後,我們有: 。
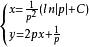 克萊羅方程
克萊羅方程因此,得到:,
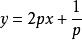 克萊羅方程
克萊羅方程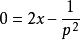 克萊羅方程
克萊羅方程為了求出奇積分,按照一般規則做出方程組: , ,
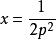 克萊羅方程
克萊羅方程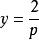 克萊羅方程
克萊羅方程由此得到: ,。
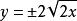 克萊羅方程
克萊羅方程所以有:。
把 y 代入原方程,可知得到的函式並不是解,因此原方程沒有奇積分。

