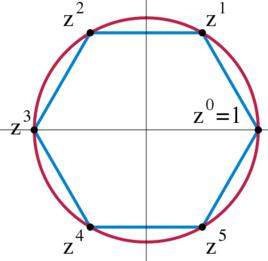
簡介
數學上，克萊因(Klein)四元群，這個定義是在1884年被菲利克斯·克萊因命名的，它是最小的非循環群。有4個元素，除單位元外其階均為2。
克萊因四元群通常以 V表示或K4表示，意為Z2×Z2，（來自德文的四元群 Vierergruppe）。它也是阿貝爾群，就是2階的循環群與自身的直積。它也同構於4階的二面體群。
講述
克萊因群的Cayley表：
克萊因四元群克萊因四元群也由群的定義介紹：
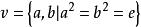克萊因四元群克萊因群的所有元素都2階的，克萊因四元群是最小的非循環群。然而，它又是一個阿貝爾群，與4階的二面體群（基數）Dih是同構的；除了2階的群以外，它是唯一的阿貝爾二面體群。
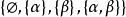克萊因四元群克萊因四元群也直接與Z2⊕Z2同構，使其可以表示為{（0,0），（0,1），（1,0），（1,1）} 的組分方式。因此，克萊因四元群是一個基本的阿貝爾2階群的例子，也稱為布爾群。因此，克萊因四元群也是由對稱差異產生的群，作為具有兩個元素的集合的冪子集上的二進制運算，即在具有四個元素的集合中。 ，在這種情況下，空集是群的本體元素。
克萊因四元群的另一個數值結構是集合{1,3,5,7}，其運算是“multiplicationmodulo 8”。這裡a是3，b是5，c = ab是3×5 = 15≡ 7。
幾何
這個十字架的對稱群是克萊因四元群。 它可以水平（a）或垂直（b）或兩者（ab）翻轉並保持不變。
在幾何學上，克萊因四元群是菱形的對稱群，矩形的對稱群不是正方形，四個元素都是本體的。
克萊因四元群在三維中有三個不同的對稱群，代表性是克萊因四元群V：
（1）一個具有三個垂直的2倍旋轉軸：D
（2）一個具有2倍旋轉軸和一個垂直的反射平面：C = D
（3）一個在反射平面（從而也在垂直的反射平面）上具有2倍旋轉軸的旋轉軸：C = D。
置換表示
克萊因四元群中的二階的三個要素是可互換的：V的自同構群是這三個元素的排列組。
克萊因四元群自己的元素的排列可以被抽象地認為是它在四點上的排列表示：
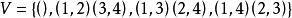克萊因四元群在該表示中，V是四個字母上的交替群A4（以及對稱組S4）的正常子群。 事實上，它是從S4到S3的同態核心。
S4內的其他表示如下：
克萊因四元群但它們不是S4的正常子群。
代數
根據伽羅瓦理論，克萊因四元群的存在（特別是其置換表示）解釋了由Lodovico Ferrari建立的計算四次方程根的公式： S4→S3對應於立方，以拉格朗日解析度計。
在有限環的建立中，有四個元素的十一個環中有八個具有克萊因四元群作為其加性子結構。
如果R×表示非零的乘法組，R +是正數的乘法組，則R××R×是環R×R的單位組，R +×R +是R××R的子組 ×（實際上是R××××××××××××××××××） 商組（R××R×）/（R +×R +）與克萊因四元群是同構的。 以類似的方式，分裂複數環的單位組除以其本體成分，也導致克萊因四元群的形成。
圖論
作為交替組A4的子組的克萊因四元群不是任何簡單圖的自動組。 然而，它是雙頂點圖形的自同構組，其中頂點以兩個邊緣彼此連線。 它也是以下簡單圖的自同構群，但是在置換表示{（），（1,2），（3,4），（1,2）（3,4）}中，其中點被標記 左上角，左下角，右上角，右下角 ：
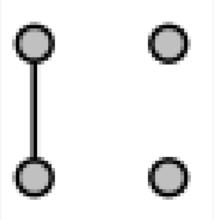克萊因四元群相關知識
若把克萊因四元群記作V = { 0, e, f, g }，其運算為加法"+"，那么以下為其運算表：
| + | 0 | e | f | g |
| o | o | e | f | g |
| e | e | 0 | g | f |
| f | f | g | 0 | e |
| g | g | f | e | 0 |
這運算是對合的：∀ x ∈ V , x + x = 0。
克萊因四元群可擴展為有限域，稱為 克萊因域，加入乘法為第二個運算，以0為零元， e為單位元。乘法與加法符合分配律。乘法表為：
| * | 0 | e | f | g |
| o | 0 | 0 | 0 | 0 |
| e | 0 | e | f | g |
| f | 0 | f | g | e |
| g | 0 | g | e | f |
克萊因四元群3個階2的元之間的對稱性，可以從它在4點上的置換表示看出：
V = < (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) >
在這表示中，V是交錯群 A的正規子群，也是4個字母上的對稱群 S的正規子群。根據伽羅瓦理論，克萊因四元群的存在，而且還具有這特別的表示，解釋了四次方程可以用根式求解的原因。
