光滑粒子法

光滑粒子法是一種拉格朗日無格線粒子方法。它利用核函式對物理問題進行近似處理，用離散的粒子來描述巨觀連續分布微觀仍為粒子的流體，而每個粒子則攜帶了其所在位置的流體的各種性質，如質量、密度、速度、能量等。

光滑粒子法[1]是一種拉格朗日無格線粒子方法。它利用核函式對物理問題進行近似處理，把連續的物質空間離散到一系列無序分布的可運動的粒子上，用離散的粒子來代替連續分布的流體，而每個粒子則攜帶了其所在位置的流體的各種性質，如質量、密度、速度、能量等。
在光滑粒子法中，用下面的積分式來表示任意函式A在ra處的值：

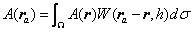
（1）
其中的函式W稱為核函式，h為光滑長度。把積分域離散成有限個粒子，每個粒子的體積為

（2）
其中分子分母分別表示粒子的質量和密度，於是（1）式可以離散成求和的形式：

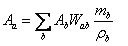
（3）
其中a、b表示粒子。
函式A的一階導數則用下式表示：

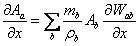
（4）
（3）和（4）是光滑粒子法的基本式，利用這兩個式子，可以把物理問題對應的控制方程離散成數值方程，然後進行數值求解。
光滑粒子法最早是用於處理天體物理問題，由Lucy（1977）和Gingold & Monaghan（1977）相互獨立地提出。之後，光滑粒子法得到迅速發展，被套用到許多領域。
[1] 光滑粒子法，英文為“Smoothed Particle Hydrodynamics Method”，簡稱“SPH method”。 關於“Smoothed Particle Hydrodynamics”的中文名，文獻中另有多種譯法，如“光滑粒子流體動力學”、“光滑粒子動力學”、“光滑質點流體力學”和“光滑質點水動力學”等。