備擇假設
 備擇假設
備擇假設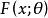 備擇假設
備擇假設 備擇假設
備擇假設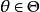 備擇假設
備擇假設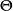 備擇假設
備擇假設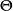 備擇假設
備擇假設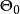 備擇假設
備擇假設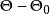 備擇假設
備擇假設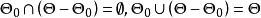 備擇假設
備擇假設設總體 的分布函式 中, 為未知參數, , 為參數空間。我們將參數空間 分解為互不相交的兩個部分 及 ,即 . 考慮檢驗問題:
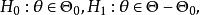 備擇假設
備擇假設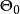 備擇假設
備擇假設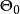 備擇假設
備擇假設 備擇假設
備擇假設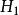 備擇假設
備擇假設為非空子集, 是假設檢驗的對象,稱 為原假設(或零假設),稱 為 備擇假設(或備選假設,對立假設)。
簡單備擇假設
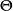 備擇假設
備擇假設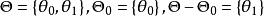 備擇假設
備擇假設如果 只含有兩個點,即若 ,則有
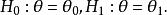 備擇假設
備擇假設 備擇假設
備擇假設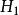 備擇假設
備擇假設這時稱 及 分別為簡單原假設及 簡單備擇假設。
複合備擇假設
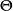 備擇假設
備擇假設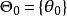 備擇假設
備擇假設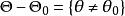 備擇假設
備擇假設如果 多於兩個點,即若 ,而 為非單點集,即有
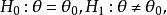 備擇假設
備擇假設 備擇假設
備擇假設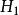 備擇假設
備擇假設則稱 為簡單原假設, 為 複合備擇假設。
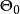 備擇假設
備擇假設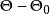 備擇假設
備擇假設 備擇假設
備擇假設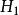 備擇假設
備擇假設註:若 及 都是非單點集,則稱 及 都是複合的。
套用-檢驗法優劣的比較
備擇假設是原假設被否定時準備接受的假設,它是按少犯第二類錯誤(見下文)來比較檢驗法優劣時必不可少的。下面做詳細闡述。
檢驗的功效
 備擇假設
備擇假設原假設的 實際的“真偽”是不知道的,是不可觀測的。人們通過一定的檢驗法基於樣本對其“真偽”作出判斷,稱為統計推斷。客觀上,存在下面4種情況。
 備擇假設
備擇假設 備擇假設
備擇假設(1) 為真,統計推斷是拒絕 ;(犯第一類錯誤,也稱“棄真錯誤”)
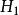 備擇假設
備擇假設 備擇假設
備擇假設(2) 為真,統計推斷是接受 ;(犯第二類錯誤,也稱“取偽錯誤”)
 備擇假設
備擇假設 備擇假設
備擇假設(3) 為真,統計推斷是接受 ;(推斷正確)
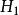 備擇假設
備擇假設 備擇假設
備擇假設(4) 為真,統計推斷是拒絕 ;(推斷正確)
情況(4)的機率稱為 檢驗的功效。顯然, 檢驗的功效=1-犯第二類錯誤的機率。
比較檢驗法優劣的原則
一個好的檢驗法應該儘可能得減小犯兩種錯誤的機率,但同時減小犯兩種錯誤的機率往往難以做到。故通常的做法是:控制犯第一類錯誤的機率,使犯第二類錯誤的機率儘可能地小(也可以說使檢驗的功效儘可能地大)。
一致最優功效檢驗(UMPT)
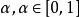 備擇假設
備擇假設 備擇假設
備擇假設依據上述比較原則,在檢驗水平為的檢驗(相當於控制了犯第一類錯誤的機率)中,功效最大者(相當於犯第二類錯誤的機率最小者)稱為水平為的一致最優功效檢驗,簡記為UMPT(Uniformly Most Powerful Test)。
備擇假設的選取
由於假設檢驗的基本原理為:在一次試驗中,小機率事件不易發生(或幾乎不可能發生),因此,我們在確立原假設與備擇假設時應遵循以下兩個原則:
 備擇假設
備擇假設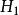 備擇假設
備擇假設 備擇假設
備擇假設(1)原假設 是在一次試驗中有絕對優勢出現的事件,而備擇假設 在一次試驗中不易發生(或幾乎不可能發生)的事件。 因此,在進行單側檢驗時,最好把原假設 取為預想結果的反面,即把希望證明的命題放在備擇假設上。
(2)將可能犯的嚴重錯誤看作第一類錯誤,因為犯第一類錯誤的機率可以控制, 犯第二類錯誤的機率是無法控制的。 如醫生對前來問診的病人作診斷時,可能會犯“有病看成無病”或者“無病看成有病”的錯誤,相比較而言,“有病看成無病”的錯誤更嚴重,故應將“問診人有病”作為原假設。 而在某項疾病普查中,將“被檢查人無病”作為原假設就不恰當了。
