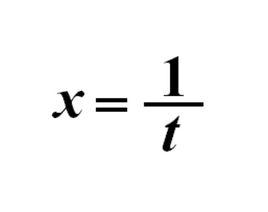定義
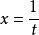 倒代換
倒代換 倒代換
倒代換 倒代換
倒代換倒代換是通過變數代換 使原來以 為自變數的數學問題變成以 為自變數的數學問題,達到降低問題難度或化簡解題過程的一種數學解題方法。
求極限
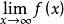 倒代換
倒代換對於形如 的極限問題,很難使用等價無窮小替代和展開泰勒公式,而等價無窮小替代和展開泰勒公式是求極限問題最有效的基本方法。
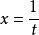 倒代換
倒代換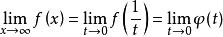 倒代換
倒代換在變數代換 下 ,可能給使用等價無窮小替代、展開泰勒公式,或使用洛必達法則帶來一定的方便
舉例
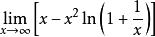 倒代換
倒代換求極限 。
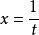 倒代換
倒代換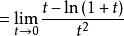 倒代換
倒代換解 作倒代換 ,原式 ,使用洛必達法則可得到
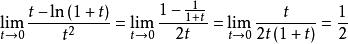 倒代換
倒代換如果使用麥克勞林展開式,則計算更為簡單
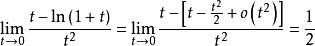 倒代換
倒代換解積分問題
不定積分問題
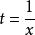 倒代換
倒代換對於不定積分問題來說,當被積函式是分母次數較高的有理函式或根式有理式時,使用倒代換也許可以使被積函式分母次數變得略低。注意,到計算最後必須把 作回代。
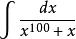 倒代換
倒代換例求不定積分 。
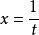 倒代換
倒代換解作倒代換 ,
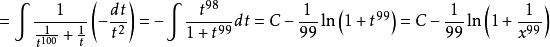 倒代換
倒代換原式 。
定積分問題
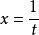 倒代換
倒代換對於定積分問題來說,當被積函式是分母次數較高的有理函式或根式有理式時,使用倒代換也許可以使被積函式分母次數變得略低。但是使用倒代換 時必須特別注意到坐標原點不能包含在積分區間之內。
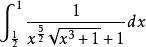 倒代換
倒代換例1求定積分 。
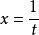 倒代換
倒代換解作倒代換 ,
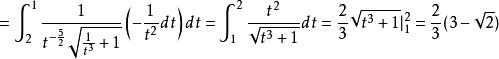 倒代換
倒代換原式 。
 倒代換
倒代換 倒代換
倒代換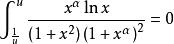 倒代換
倒代換例2 對於任意實數 ,和任一正實數 ,證明 。
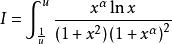 倒代換
倒代換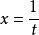 倒代換
倒代換證 明 記 ,則在倒代換 下,有
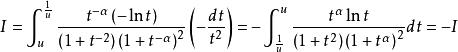 倒代換
倒代換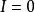 倒代換
倒代換可得 ,證畢。
廣義積分問題
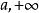 倒代換
倒代換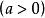 倒代換
倒代換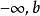 倒代換
倒代換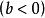 倒代換
倒代換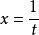 倒代換
倒代換在[ ) 或( ] 上有界函式的廣義積分問題可通過倒代換 變為有界區間上的定積分問題。這樣至少為廣義積分的數值近似計算創造了條件。
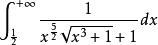 倒代換
倒代換例1求 。
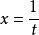 倒代換
倒代換解作倒代換 ,
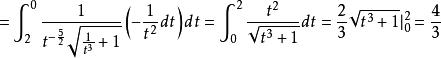 倒代換
倒代換原式 。
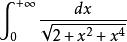 倒代換
倒代換例2 通過換元法將廣義積分 轉化為適宜於數值計算的形式
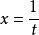 倒代換
倒代換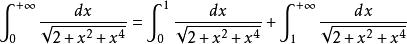 倒代換
倒代換解作倒代換 ,則 ,
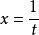 倒代換
倒代換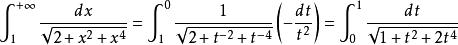 倒代換
倒代換對上式第二項作倒代換 ,可得 ,,
這樣就得到了原廣義積分適宜於數值計算的形式
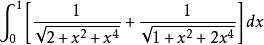 倒代換
倒代換