定理
定理(英語:Theorem)是經過受邏輯限制的證明為真的陳述。一般來說,在數學中,只有重要或有趣的陳述才叫定理。證明定理是數學的中心活動。
雖然定理可在命題邏輯的框架下完全用符號寫成,但它們還是多數用自然語言(例如漢語)表達。證明亦然,也是以有邏輯和有組織的方式,用含意清晰的文字陳述出一個(非正式的)論證,使得讀者能夠理解並跟隨整個證明的脈胳,以至最終對命題真確性的信服。如有必要的話,也可從原本文字重構出(正式的)符號形式的論證。文字形式的論證顯然要比純符號方便人們閱讀—而事實上,數學家往往也偏好某些證明,它們除了顯示命題為真之外,更是從某種角度解釋了為何命題必須為真。有時候,一張圖的勾勒就足以證明一個定理。因為定理及其證明是處於數學的核心,它們很大程度上也是數學之美的體現。定理有時被描述為”平凡” 、” 困難”,或者” 深入” ,而更甚是” 美麗” 。這些主觀判斷不只因人而異,且隨著時間推移也可能有變:就例如,由於證明被簡化或變得更易懂,本來顯得困難的原命題也變成平凡的了。另一方面,一個深邃的定理可以被簡單地表述,但其證明可以揭示出數學領域間叫人驚奇,而又微妙的隱秘關係。費馬最後定理正是如此的一個典型例子。
逆定理
逆定理是將某一定理的條件和結論互換所得的定理就是原來定理的逆定理。如:“在一個三角形中,如果兩條邊相等,它們所對應的角也相等。它的逆定理是:“在一個三角形中,如果兩個角相等,則它所對應的邊也相等。”
定義
一個命題是真命題,它的逆命題卻不一定是真命題。如果一個定理的逆命題經過證明是真命題,那么它也是一個定理,這兩個定理稱為 互逆定理。
互逆定理典例
1、直角三角形中,兩直角邊的平方和等於斜邊的平方。(勾股定理)
其逆定理:如果一個三角形兩直角邊的平方和等於斜邊的平方,那么這個三角形是直角三角形。
2、平行四邊形的對角線互相平分。
其逆定理:如果一個四邊形對角線互相平分,那么這個四邊形是平行四邊形。
3、角平分線上的點到角的兩邊的距離相等。
其逆定理:如果某一點到角的兩邊距離相等,那么這個點在角平分線上。
套用
數學知識是一個有機整體,許多知識點有著內在辯證統一的聯繫,而“勾股定理的逆定理”是在“勾股定理”研究的基礎上形成的。兩個定理不但組成一對完善的互逆定理,而且在研究過程中亦展現了數學知識內部發展、運動的辯證統一關係。數學教學中,要充分地揭示兩定理的互逆性和統一性,加深學生對勾股定理本質的認識,進而親身體驗矛盾轉化的美感。
 互逆定理
互逆定理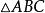 互逆定理
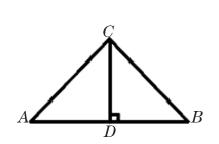
互逆定理例題:如圖, 中,CD是邊AB上的高。
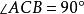 互逆定理
互逆定理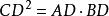 互逆定理
互逆定理(1)若 ,求證 。
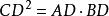 互逆定理
互逆定理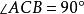 互逆定理
互逆定理(2)若 ,求證 。
證明:
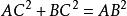 互逆定理
互逆定理(1)由勾股定理得:
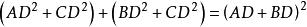 互逆定理
互逆定理所以
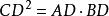 互逆定理
互逆定理化簡得:
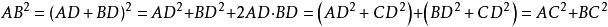 互逆定理
互逆定理(2)
由勾股定理的逆定理可得
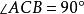 互逆定理
互逆定理。

