定義
命題
命題的定義:一般的,在數學中把用語言、符號或式子表達的,可以判斷真假的陳述句叫做命題。其中判斷為真的語句叫做真命題,判斷為假的語句叫做假命題。
每一個命題都有逆命題,只要將原命題的題設改成結論,並將結論改成題設,便可得到原命題的逆命題。但是原命題正確,它的逆命題未必正確。例如真命題“對頂角相等”的逆命題為“相等的角是對頂角”,此命題就是假命題。
互逆命題
互逆命題的定義:如果一個命題的條件與結論分別是另一個命題的結論與條件,那么這兩個命題稱為互逆命題。如把其中一個稱為原命題,那么另一個稱為它的逆命題。其中一個命題稱為另一個命題的逆命題。把一個命題的條件和結論互換就得到它的逆命題,所以每個命題都有逆命題。
逆否命題
逆否命題的定義:一個命題的條件和結論分別是另一個命題的條件的否定和結論的否定,把這樣的兩個命題叫做互否命題。如果把其中一個稱為原命題,那么另一個就叫做它的否命題。
性質
(1)原命題和逆命題為互逆命題;
(2)逆否命題和否命題為互逆命題;
(3)兩個命題為互逆命題,它們的真假性沒有關係。
例如:
(1)原命題:“若a=0,則ab=0”,為真命題;
逆命題:“若ab=0,則a=0”,為假命題。
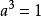 互逆命題
互逆命題(2)原命題:“若a=1,則 ”,為真命題;
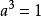 互逆命題
互逆命題逆命題:“若 ,則a=1”,為真命題。
與互逆定理
互逆命題:在兩個命題中,如果一個命題的條件和結論分別是另一個命題的結論和條件,那么這兩個命題稱為互逆命題。如果把其中一個命題叫做原命題,那么另一個命題就叫做逆命題。把一個命題的條件和結論互換就得到它的逆命題,所以每個命題都有逆命題。
互逆定理:如果一個定理的逆命題經過證明是真命題,那么它也是一個定理,這兩個定理稱為互逆定理。
互逆命題的概念大於互逆定理。互逆定理是互逆命題,但互逆命題未必是互逆定理。
關係
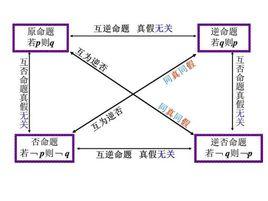
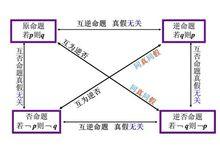
原命題、逆命題、否命題和逆否命題四種命題有如下關係。
 互逆命題
互逆命題相互關係
四種命題的相互關係如下:
(1)原命題與逆命題互逆;
(2)否命題與原命題互否;
(3)原命題與逆否命題相互逆否;
(4)逆命題與否命題相互逆否;
(5)逆命題與逆否命題互否;
(6)逆否命題與否命題互逆 。
真假關係
四種命題的真假關係如下:
(1)兩個命題互為逆否命題,它們有相同的真假性(原命題與逆否命題同真同假,逆命題與否命題同真同假);
(2)兩個命題為互逆命題或互否命題,它們的真假性沒有關係 。
| 原命題 | 逆命題 | 否命題 | 逆否命題 |
| 真 | 真 | 真 | 真 |
| 真 | 假 | 假 | 真 |
| 假 | 真 | 真 | 假 |
| 假 | 假 | 假 | 假 |