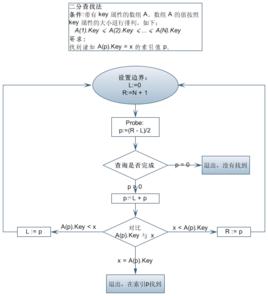
查找過程
首先,假設表中元素是按升序排列,將表中間位置記錄的關鍵字與查找關鍵字比較,如果兩者相等,則查找成功;否則利用中間位置記錄將表分成前、後兩個子表,如果中間位置記錄的關鍵字大於查找關鍵字,則進一步查找前一子表,否則進一步查找後一子表。重複以上過程,直到找到滿足條件的記錄,使查找成功,或直到子表不存在為止,此時查找不成功。
算法要求
1.必須採用順序存儲結構。
2.必須按關鍵字大小有序排列。
比較次數
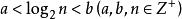 二分查找
二分查找計算公式:
當順序表有n個關鍵字時:
查找失敗時,至少比較a次關鍵字;查找成功時,最多比較關鍵字次數是b。
注意:a,b,n均為正整數。
算法複雜度
二分查找的基本思想是將n個元素分成大致相等的兩部分,取a[n/2]與x做比較,如果x=a[n/2],則找到x,算法中止;如果x<a[n/2],則只要在數組a的左半部分繼續搜尋x,如果x>a[n/2],則只要在數組a的右半部搜尋x.
時間複雜度無非就是while循環的次數!
總共有n個元素,
漸漸跟下去就是n,n/2,n/4,....n/2^k(接下來操作元素的剩餘個數),其中k就是循環的次數
由於你n/2^k取整後>=1
即令n/2^k=1
可得k=log2n,(是以2為底,n的對數)
所以時間複雜度可以表示O(h)=O(log2n)
下面提供一段二分查找實現的偽代碼:
BinarySearch(max,min,des)
mid-<(max+min)/2
while(min<=max)
mid=(min+max)/2
if mid=des then
return mid
elseif mid >des then
max=mid-1
else
min=mid+1
return max
折半查找法也稱為二分查找法,它充分利用了元素間的次序關係,採用分治策略,可在最壞的情況下用O(log n)完成搜尋任務。它的基本思想是:(這裡假設數組元素呈升序排列)將n個元素分成個數大致相同的兩半,取a[n/2]與欲查找的x作比較,如果x=a[n/2]則找到x,算法終止;如 果x<a[n/2],則我們只要在數組a的左半部繼續搜尋x;如果x>a[n/2],則我們只要在數組a的右 半部繼續搜尋x。
代碼示例
C#代碼
Go原始碼
Swift原始碼
Python原始碼
pascal原始碼
第一種
第二種
C和C++代碼
<C和C++的語法基本相同>
循環實現
第一種
第二種
第三種
遞歸實現(可直接編譯)
Java代碼
AAuto代碼
PHP代碼
AS3代碼
JavaScript代碼
PHP代碼