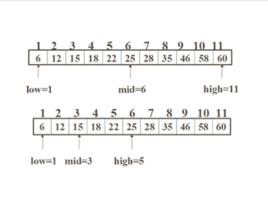
程式介紹
折半查找法是效率較高的一種查找方法。假設有已經按照從小到大的順序排列好的五個整數a0~a4,要查找的數是X,其基本思想是: 設查找數據的範圍下限為l=0,上限為h=4,求中點m=(l+h)/2,用X與中點元素am比較,若X等於am,即找到,停止查找;否則,若X大於am,替換下限l=m+1,到下半段繼續查找;若X小於am,換上限h=m-1,到上半段繼續查找;如此重複前面的過程直到找到或者l>h為止。如果l>h,說明沒有此數,列印找不到信息,程式結束。
該方法是查找的範圍不斷縮小一半,所以查找效率較高。
加倍折半法 的關鍵是如何“加倍”、“折半”。那么“加倍”、“折半”的方法又是什麼呢?傳統的“加倍”的方法,是將線段延長一倍;傳統的“折半”的方法,是取線段的中點。豈不知,“三角形中位線定理”、“直角三角形斜邊上的中線等於斜邊的一半”、“等腰三角形的三線合一性質”、“平行線等分線段定理”……均有“加倍、折半”的功用。也就是說“加倍”“折半”的方法是眾多的、豐富的。而這些的方法基本上都是來自上述的一些重要的定理。
例1 已知:△ABC中,AB=AC,延長AB到D,使DB=AB,E是AB的中點。求證:CD=2CE
思路一:延長CE到F1,使EF1=CE,即用
延長的方法將CE擴大一倍為CF1,證CF1=CD
思路二:取CD的中點,即用“取中點”的方法將CD縮小一半為CF2,證CF2=CE。
以上為“傳統”的加倍折半法,引申後則有:
思路三:抓住E為AB中點這一特點,作△ABF3,使CE為該三角形的中位線(過A作AF3∥CE,交BC的延長線於F3),即用三角形中位線定理將CE擴大一倍為AF3,證AF3=CD
思路四:抓住B為AD中點這一特點,作△ADC以CD邊為底邊的中位線(過B作BF4∥CD,交AC於F4),即:用三角形中位線定理將CD縮小一半為BF4,證BF4=CE
引申
對三角形加倍折半法“用途”的引申
傳統的加倍折半法主要套用於線段(或角)倍半關係的證明。隨著“方法”的引申,其功能也隨之得到了增強。特別是完全領會了加倍折半法的基本思想後,許多疑難問題就會迎刃而解。它的用途遠遠超出了原先的範圍,幾乎適用於所有含“2”的類型題。下面,分“結論中含有2”和“題設中含有2”兩中情況作簡單的介紹。
1、加倍折半法來解“結論中含有2”的類型題,實際上就是“分析法”的一種具體套用。“加倍折半法”在此起的作用,也可稱之為“解題技巧”。例1屬於該種類型的“傳統”例題,下面舉幾個引申後的例子。
例2 已知:△ABC中,D是BC上的中點,F是AD上的任意一點,延長CF交AB於E。求證:AF:DF=2AE:BE
思路:本題的難點是如何除去比例式中的“2”
方法一:將AE或DF“加倍”,由於D是BC的中點,
過點B作BG∥DF,交CE的延長線於G,則用三角形中位線定理將DF“擴大一倍”為BG。這樣,原題就有效的轉化為證明AF:BG=AE:BE。
方法二:是將AF或BE“折半”,由於D是BC的中點,過點D作DH∥AB,交CE於GH,則用三角形中位線的定理將BE“縮小一半”為DH。這樣,原題就有效的轉化為證明AF:DF=AE:DH。
2、用加倍折半法來解“題設中含有2”的類型題,實際上就是“綜合法”的一種具體的套用。“加倍折半法”在此起的作用,可稱之為“解題經驗”。
例3 已知:△ABC中,AD是高線,∠ABC=2∠ACB。求證:CD=AB+BD
思路:該題屬於“截長補短法”的習題,
但由於已知條件中有角的倍半關係,因
而用“加倍折半法”的思路也可以解決。
思路一:延長DB到E1,使BE1=BA(造等腰三角形將∠ABC“折半“為E1),則∠E1=∠C,AE1=AC,CD=DE1,故CD=AB+BD
思路二:作∠CAE2,使∠CAE2=∠C(造等腰三角形將∠C“加倍”為∠AE2B),則∠AE2B=∠ABC,AE2=E2C=AB,BD=DE2,故CD=AB+BD。
優缺點
Bentley在他的著作《Writing Correct Programs》中寫道,90%的計算機專家不能在2小時內寫出完全正確的二分搜尋算法。問題的關鍵在於準確地制定各次查找範圍的邊界以及終止條件的確定,正確地歸納奇偶數的各種情況,其實整理後可以發現它的具體算法是很直觀的。
折半查找法的優點是比較次數少,查找速度快,平均性能好;
其缺點是要求待查表為有序表,且插入刪除困難。
因此,折半查找方法適用於不經常變動而查找頻繁的有序列表。
算法步驟描述
① 首先確定整個查找區間的中間位置 mid = ( left + right )/2 。
② 用待查關鍵字值與中間位置的關鍵字值進行比較; 若相等,則查找成功 若大於,則在後(右)半個區域繼續進行折半查找 若小於,則在前(左)半個區域繼續進行折半查找。
③ 對確定的縮小區域再按折半公式,重複上述步驟。最後,得到結果:要么查找成功, 要么查找失敗。折半查找的存儲結構採用一維數組存放 。
基本算法實現
函式
bin_search(int A[],int n,int key){
int low,high,mid;
low = 0;
high = n-1;
while(low<=high)
{
mid =(low + high)/2;
if(A[mid]==key)return mid;
if(A[mid]<key){
low =mid + 1;
}
if(A[mid]>key){
high= mid - 1;
}
}
return -1;
}
C語言實現代碼
#include <stdio.h>int main()
{
int a[11]={0,1,2,3,4,5,6,7,8,9,10},min=0,max=10,mid,n; //max為數列長度,a[0]作為第一個數組元素
printf("請輸入您要查找的數:\n");
scanf("%d",&n);
while(min+1!=max)
{
mid=(min+max)/2;
if (n>a[mid]) min=mid;
else if (n<a[mid]) max=mid;
else
{
printf("輸入的數在數列的第%d位\n",mid);
exit(0);
}
}
if(n==a[max])
{
max+=1;
printf("\n輸入的數在數列的第%d位\n",max);
}
else if(n==a[min])
{
min+=1;
printf("\n輸入的數在數列的第%d位\n",min);
}
else if(n!=a[mid])
printf("\n輸入的數不在數列中");
}
Dev-c++實現
#include <stdio.h>
#include <stdlib.h>
void main()
{
int a[15]={1,2,3,4,5,6,7,8,9,10,11,12,13,15};
int n,m,top,bot,mid;
top=m=1; //此處修改top=0;m=1;
bot=14;
printf("please input a number:");
scanf("%d",&n);
while(top<=bot)
{
mid=(top+bot)/2;
if(n==a[mid])
{
printf("這是第%d個元素的值。\n",mid+1);
m=0;
break;
}
else if(n>a[mid])
top=mid+1;
else if(n<a[mid])
bot=mid-1;
}
if(m)
printf("無此數。\n");
system("PAUSE");
return 0;
}