“小九九”的由來
九九乘法口訣表現在小學生學的“小九九”口訣，是從“一一得一”開始，到“九九八十一”為止，而在古代，卻是倒過來，從“九九八十一”起，到“二二得四”止。因為口訣開頭兩個字是“九九”，所以，人們就把它簡稱為“小九九”。大約到13、14世紀的時候才倒過來像現在這樣“一一得一……九九八十一”。
中國使用“九九口訣”的時間較早。在《荀子》、《管子》、《淮南子》、《戰國策》等書中就能找到“三九二十七”、“六八四十八”、“四八三十二”、“六六三十六”等句子。由此可見，早在“春秋”、“戰國”的時候，《九九乘法歌訣》就已經開始流行了。
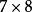九九乘法口訣表
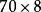九九乘法口訣表
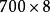九九乘法口訣表 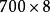九九乘法口訣表
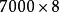九九乘法口訣表
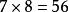九九乘法口訣表
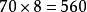九九乘法口訣表
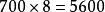九九乘法口訣表
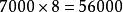九九乘法口訣表 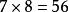九九乘法口訣表古希臘、古埃及、古印度、古羅馬沒有進位制，原則上需要無限大的乘法表，因此不可能有九九表。例如希臘乘法表必須列出 ， ， ， ， ……。相形之下，由於九九表基於十進位制， ， ， ， ，只需 一項代表。
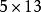九九乘法口訣表古埃及沒有乘法表。考古家發現，古埃及人是通累次迭加法來計算乘積的。例如計算 ,先將13+13得26，再迭加26+26=52，然後再加上13得65。
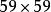九九乘法口訣表
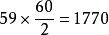九九乘法口訣表 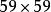九九乘法口訣表 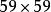九九乘法口訣表
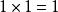九九乘法口訣表
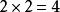九九乘法口訣表
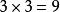九九乘法口訣表
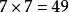九九乘法口訣表
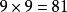九九乘法口訣表
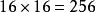九九乘法口訣表
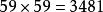九九乘法口訣表
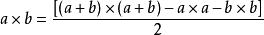九九乘法口訣表
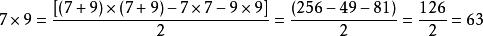九九乘法口訣表巴比倫算術有進位制，比希臘等幾個國家有很大的進步。不過巴比倫算術採用60進位制，原則上一個“ ”乘法表需要 項；由於“ ”乘法表太龐大，巴比倫人從來不用類似於九九表的“乘法表”。考古學家也從來沒有發現類似於九九表的“ ”乘法表。不過，考古學家發現巴比倫人用獨特的 , , …… ,…… …… …… 的“平方表”。要計算兩個數a,b的乘積，巴比倫人則依靠他們最擅長的代數學， 。例如 .
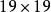九九乘法口訣表古瑪雅人用20進位制，跟現代世界通用的十進位制最接近。一個 乘法表有190項，比九九表的45項雖然大三倍多，但比巴比倫方法還是簡便得多。可是考古學家至今還沒有發現任何瑪雅乘法表。
用乘法表進行乘法運算，並非進位制的必然結果。巴比倫有進位制，但它們並沒有發明或使用九九表式的乘法表，而是發明用平方表法計算乘積。瑪雅人的數學是西半球古文明中最先進的，用20進位制，但也沒有發明乘法表。可見從進位制到乘法表是一個不少的進步。
中國春秋戰國時代不但發明了十進位制，還發明九九表。後來東傳入高麗、日本，經過絲綢之路西傳印度、波斯，繼而流行全世界。十進位制和九九表是古代中國對世界文化的一項重要的貢獻。今日世界各國較少使用希臘等國的乘法。
九九表的特點
1、九九表一般只用一到九這9個數字。
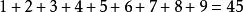九九乘法口訣表2、九九表包含乘法的可交換性，因此只需要八九七十二，不需要“九八七十二”，9乘9有81組積，九九表只需要 項積。明代珠算也有採用81組積的九九表。45項的九九表稱為小九九，81項的九九表稱為大九九。
3、古代世界最短的乘法表。瑪雅乘法表須190項，巴比倫乘法表須1770項，埃及、希臘、羅馬、印度等國的乘法表須無窮多項；九九表只需45/81項。
4、朗讀時有節奏，便於記憶全表。
5、九九表存在了至少三千多年。從春秋戰國時代就用在籌算中運算，到明代則改良並用在算盤上。現在，九九表也是國小算術的基本功。
數學版乘法口訣表
| 1×1=1 | ||||||||
| 1×2=2 | 2×2=4 | |||||||
| 1×3=3 | 2×3=6 | 3×3=9 | ||||||
| 1×4=4 | 2×4=8 | 3×4=12 | 4×4=16 | |||||
| 1×5=5 | 2×5=10 | 3×5=15 | 4×5=20 | 5×5=25 | ||||
| 1×6=6 | 2×6=12 | 3×6=18 | 4×6=24 | 5×6=30 | 6×6=36 | |||
| 1×7=7 | 2×7=14 | 3×7=21 | 4×7=28 | 5×7=35 | 6×7=42 | 7×7=49 | ||
| 1×8=8 | 2×8=16 | 3×8=24 | 4×8=32 | 5×8=40 | 6×8=48 | 7×8=56 | 8×8=64 | |
| 1×9=9 | 2×9=18 | 3×9=27 | 4×9=36 | 5×9=45 | 6×9=54 | 7×9=63 | 8×9=72 | 9×9=81 |
