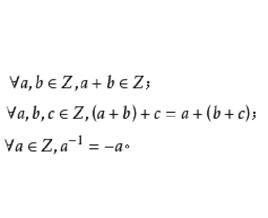基本介紹
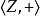 整數加法群
整數加法群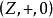 整數加法群
整數加法群整數及整數上的加法運算構成了群(有的書籍寫做),稱之為 整數加法群。其中0是群的單位元,每一個元素的逆元是它的相反數。
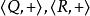 整數加法群
整數加法群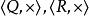 整數加法群
整數加法群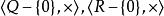 整數加法群
整數加法群 整數加法群
整數加法群整數與整數上的乘法運算不能構成群,因為除了元素1和-1外,所有元素都不存在逆元。類似地,都是群,而都不是群,因為元素0沒有逆元。都是群,兩個群的單位元均為1,元素的逆元是該元素的倒數 。
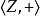 整數加法群
整數加法群整數加法群,是由整數Z和整數加法運算+組成。其單位元0;
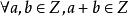 整數加法群
整數加法群封閉性 :;
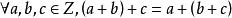 整數加法群
整數加法群結合律:;
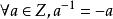 整數加法群
整數加法群逆元:。
相關性質
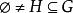 整數加法群
整數加法群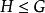 整數加法群
整數加法群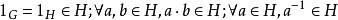 整數加法群
整數加法群① 子群設G是群,,若H具封閉性、單位元、逆元,稱H是G的一個子群,記號。換句話說,若,則H是G的一個 子群。作為群公理之一的結合律,因為H繼承了G的運算,所以自然成立,因此,子群也是群。
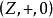 整數加法群
整數加法群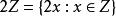 整數加法群
整數加法群 整數加法群
整數加法群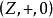 整數加法群
整數加法群考慮整數加法群,自然可以想到,在偶整數上做加法可以成群,如0+2=2,2+4=6…定義為整數上的所有偶數,則是的子群。
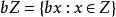 整數加法群
整數加法群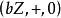 整數加法群
整數加法群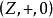 整數加法群
整數加法群事實上,對任意整數b,定義,則是的子群。
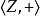 整數加法群
整數加法群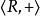 整數加法群
整數加法群整數加法群是的子群 。
 整數加法群
整數加法群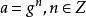 整數加法群
整數加法群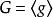 整數加法群
整數加法群② 循環群 設g是群G中一個取定的元素,若群G的任意一個元素可以寫成的形式,則稱G循環群,稱g為群G的一個生成元,可寫成。
循環群(cyclic group)是一種重要的群,即由一個元素生成的群。循環群分為兩類:一類是有限循環群,n個元的有限循環群與模n的剩餘類加群同構;另一類是無限循環群,它與整數加法群同構,循環群是特殊的阿貝爾群,循環群的子群和商群仍是循環群。
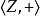 整數加法群
整數加法群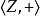 整數加法群
整數加法群整數加法群中,任意元素a都可以表示成1或-1的冪,因此是循環群。
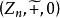 整數加法群
整數加法群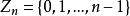 整數加法群
整數加法群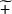 整數加法群
整數加法群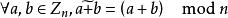 整數加法群
整數加法群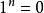 整數加法群
整數加法群 整數加法群
整數加法群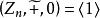 整數加法群
整數加法群在整數加法群上做一些小修改可以做出另一個有意思的循環群,其中,同餘加法定義為。在這裡,也就是說(n個1相加模n餘0)。所以,是n階循環群。
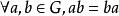 整數加法群
整數加法群③ 交換群 具有交換性的群稱為 交換群。交換性:。
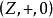 整數加法群
整數加法群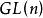 整數加法群
整數加法群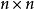 整數加法群
整數加法群整數加法群是交換群,因為整數加法滿足交換律。一般線性群由所有的可逆矩陣和矩陣乘法組成,它不是交換群,因為矩陣乘法不滿足交換律 。
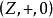 整數加法群
整數加法群④在整數加法群中,0的周期是1,除0以外的其他元素的周期都是無限的。
群公理
在數學中,群是一種代數結構,由一個集合S與一個二元運算 ·組成,要成為群,還需要滿足一些條件,這些條件被稱為“ 群公理”,即 封閉性、 結合律、 單位元和 逆元。
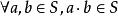 整數加法群
整數加法群1.封閉性,即。
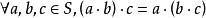 整數加法群
整數加法群2.結合律,即。
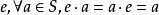 整數加法群
整數加法群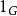 整數加法群
整數加法群3.單位元,即有一個元素(在群G中常用或1表示單位元)。
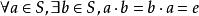 整數加法群
整數加法群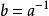 整數加法群
整數加法群4.逆元,即,記。
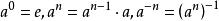 整數加法群
整數加法群可以定義元素a的冪為:。
值得注意的是,二元運算 ·僅表示抽象的運算符號,在不同的群中解釋不同。在不引起歧義的情況下經常將符號 ·省略 。