中心矩：對於正整數k，如果E(X)存在，且E[|X-E(X)]
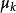中心矩對於一維隨機變數X，其k階 中心矩為相對於X之期望值的k階矩：
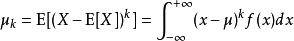中心矩前幾階中心矩具有較直觀的意義。
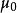中心矩第0階中心矩 恆為1。
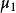中心矩第1階中心矩 恆為0。
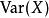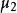中心矩
中心矩第2階中心矩 為X的方差。
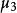中心矩第3階中心矩 用於定義X的偏度。
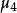中心矩第4階中心矩 用於定義X的峰度。
中心矩具有平移不變性。對於任意的隨機變數X和任意常數c，恆有：
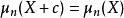中心矩n階中心矩是 n次齊次函式。
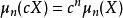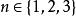中心矩
中心矩只有當 ，且X和Y為兩個互相獨立的隨機變數時，中心矩才具有加法性。
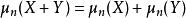中心矩
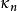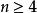中心矩
中心矩另一個與中心矩類似，但在 時仍保有加法性的統計量為 n階累積量。
隨機變數（或統計量，下同）的期望定義為其1階原點矩：
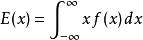中心矩在方差等定義中，期望也稱為隨機變數的“中心”。顯然，任何隨機變數的1階中心矩為0。
隨機變數的方差定義為其2階中心矩：
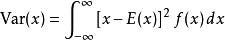中心矩隨機變數的偏態定義為其3階中心矩：
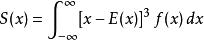中心矩隨機變數的峰態定義為其4階中心矩：
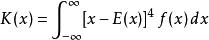中心矩原點矩 中心矩 原點矩 原點矩 原點矩 設隨機變數X的函式 的數學期望存在，則稱 為X的k階中心矩 ，記作 ，即 原點矩 原點矩 原點矩 易知，一階中心矩恆等於零，即 ；二階中心矩就是方差，即 。 關係原點矩與中心矩...
基本介紹 中心矩 關係 舉例定義統計上是用四階中心矩來測定峰度的。因為實驗研究表明，偶階中心矩的大小與圖形分布的峰度有關。其中的二階中心矩就是數據的方差，它在一定程度上...中心矩來反映分布的尖峭程度。為了消除變數值水平和計量單位不同的影響，實際...
定義 公式標準化數據序列的四階中心矩。所以，在相同的標準差下，峰度係數越大，分布...。 定義四階標準矩可以定義為： 峰度 其中μ是四階中心矩...四階中心矩除以機率分布方差的平方再減去3： 峰度 這也被稱為超值峰度...
含義 定義 樣本峰度 套用M0有很大的隨機性。二、使用三階中心矩計量的偏度係數該偏度係數是用三階中心矩除以標準差的三次方來度量偏斜程度，記為α，計算公式為 使用三階中心距計量的偏度係數 稱為三階中心矩。偏度係數 可以適用任何數據。α 和SK...
;MajorAxisLength' 與區域具有相同標準二階中心矩...' 與區域具有相同標準二階中心矩的橢圓的短軸長度（像素意義下） 'Eccentricity' 與區域具有相同標準二階中心矩...
=1，2，...存在，則稱它為X的k階中心矩。若E{(X^k）（Y^p...，則稱它為X和Y的k+l階混合中心矩。顯然，X的數學期望E(X)是X的一階原點矩，方差D(X)是X的二階中心矩，協方差Cov(X，Y)是X和Y...
定義 性質 矩陣 套用中心矩來估計總體的方差。由來它是由英國統計學家皮爾遜Pearson...常用的數字特徵，主要有中心矩和原點矩。 由辛欽大數定律知，簡單隨機樣本...外在統計學中還有二階中心矩（方差）。 ...
概述 由來 優點 類別從矩狀態結構中提取中心矩 double cvGetCentralMoment( cvMoments* moments, int... cvGetCentralMoment 提取中心矩，其中圖像矩的定義...
