百科名片
 協方差
協方差協方差分析是建立在方差分析和回歸分析基礎之上的一種統計分析方法。 方差分析是從質量因子的角度探討因素不同水平對實驗指標影響的差異。一般說來,質量因子是可以人為控制的。 回歸分析是從數量因子的角度出發,通過建立回歸方程來研究實驗指標與一個(或幾個)因子之間的數量關係。但大多數情況下,數量因子是不可以人為加以控制的。
屬性
兩個不同參數之間的方差就是協方差 若兩個隨機變數X和Y相互獨立,則E[(X-E(X))(Y-E(Y))]=0,因而若上述數學期望不為零,則X和Y必不是相互獨立的,亦即它們之間存在著一定的關係。
定義
E[(X-E(X))(Y-E(Y))]稱為隨機變數X和Y的協方差,記作Cov(X,Y),即Cov(X,Y)=E[(X-E(X))(Y-E(Y))]。
協方差與方差之間有如下關係:
D(X+Y)=D(X)+D(Y)+2Cov(X,Y)
D(X-Y)=D(X)+D(Y)-2Cov(X,Y)
協方差與期望值有如下關係:
Cov(X,Y)=E(XY)-E(X)E(Y)。
協方差的性質:
(1)Cov(X,Y)=Cov(Y,X);
(2)Cov(aX,bY)=abCov(X,Y),(a,b是常數);
(3)Cov(X+X,Y)=Cov(X,Y)+Cov(X,Y)。
由協方差定義,可以看出Cov(X,X)=D(X),Cov(Y,Y)=D(Y)。
協方差作為描述X和Y相關程度的量,在同一物理量綱之下有一定的作用,但同樣的兩個量採用不同的量綱使它們的協方差在數值上表現出很大的差異。為此引入如下概念:
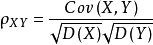 協方差
協方差定義
稱為隨機變數X和Y的(Pearson)相關係數。
定義
若ρXY=0,則稱X與Y不線性相關。
即ρXY=0的充分必要條件是Cov(X,Y)=0,亦即不相關和協方差為零是等價的。
定理
設ρXY是隨機變數X和Y的相關係數,則有
(1)∣ρ∣≤1;
(2)∣ρ∣=1充分必要條件為P{Y=aX+b}=1,(a,b為常數,a≠0)
定義
設X和Y是隨機變數,若E(X^k),k=1,2,...存在,則稱它為X的k階原點矩,簡稱k階矩。
若E{[X-E(X)]},k=1,2,...存在,則稱它為X的k階中心矩。
若E{(X^k)(Y^p)},k、l=1,2,...存在,則稱它為X和Y的k+p階混合原點矩。
若E{[X-E(X)]^k[Y-E(Y)]^l },k、l=1,2,...存在,則稱它為X和Y的k+l階混合中心矩。
顯然,X的數學期望E(X)是X的一階原點矩,方差D(X)是X的二階中心矩,協方差Cov(X,Y)是X和Y的二階混合中心矩。
農業套用
協方差在農業上的套用
農業科學實驗中,經常會出現可以控制的質量因子和不可以控制的數量因子同時影響實驗結果的情況,這時就需要採用協方差分析的統計處理方法,將質量因子與數量因子(也稱協變數)綜合起來加以考慮。
比如,要研究3種肥料對蘋果產量的實際效應,而各棵蘋果樹頭年的“基礎產量”不一致,但對試驗結果又有一定的影響。要消除這一因素帶來的影響,就需將各棵蘋果樹第1年年產量這一因素作為協變數進行協方差分析,才能得到正確的實驗結果。
當兩個變數相關時,用於評估它們因相關而產生的對應變數的影響。
當多個變數獨立時,用方差來評估這種影響的差異。
當多個變數相關時,用協方差來評估這種影響的差異。