基本介紹
定義 保持原點不變的仿射變換叫做中心仿射變換，它的坐標表示是
中心仿射變換群前面講過的向X軸或向Y軸的壓縮是中心仿射變換的特例 。
定義向X軸和向Y軸的壓縮的積所得到的變換
中心仿射變換群叫做伸縮變換。
顯然伸縮變換也是中心仿射變換的特例。
下面給出中心仿射變換的另一個特殊形式，錯切變換的定
定義坐標表示式是
中心仿射變換群和
中心仿射變換群的仿射變換，前者叫做平面上沿X軸的錯切變換，後者叫做平面上沿y軸的錯切變換。
圖1表示矩形經過向X軸的錯切變換後所得的圖形。
容易驗證所有中心仿射變換構成群 。
圖1中心仿射群
仿射幾何是由線性變換群
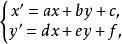中心仿射變換群制約的。這種變換可以認為是
中心仿射變換群和平移複合而成的 。上面像T的這種變換稱為 齊次仿射變換或 中心仿射變換，這種變換構成的集稱為 齊次仿射群或 中心仿射群。用“中心的"這個形容詞是因為原點或“中心”在這種變換下不變(用x=0，y=0代入即得)。式中a,b,d,e是實參數，並且滿足ae-bd≠0。加上這個條件的原因是：由T的變換公式可以從x和y算出x'和y'，但在ae-bd=0時，這並非克萊因
中心仿射變換群的變換。當ae-bd≠0時，讀者用中學代數中解二元一次方程組的辦法可從T的變換式由x'和y'算出x和y。因而這時T是個變換(一對一的到上映照)。注意，旋轉是一種特殊的仿射變換，此時a=e=cosθ，b=sinθ，d=-sinθ，而ae-bd=cos θ+sin θ=1 。
