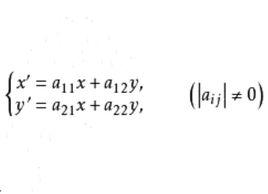定義
中心仿射變換是指含一個不變點的仿射變換，這個不變點稱為中心仿射變換的中心。在以變換中心為坐標原點的仿射坐標系中，中心仿射變換公式右端的常數項為0。例如，在平面仿射坐標系中，變換
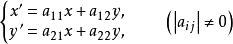中心仿射變換是一個中心仿射變換，其變換中心為坐標原點 。
在平面和空間的變換下，可以有—些點或圖形的象就是它們自己，這就是說它倆並不被變換所改變，因此我們把這種點或圖形叫做已知變換的不變的點或圖形。有一個不變點的仿射變換叫做中心仿射變換，不變點就叫做變換的中心。假如取一個中心仿射變換的中心作為坐標原點，則變換公式左邊就沒有了自由項。因此我們知道，以坐標原點作為中心的中心仿射變換的公式是
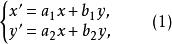中心仿射變換或
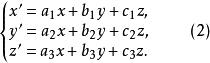中心仿射變換變換公式(1)或(2)右邊是齊次的，在代數上叫做齊次線性變換。因此，以坐標原點作為中心的中心仿射變換的公式是行列式不等於零的齊次線性變換。反之，行列式不等於零的齊次線性變換總表示中心仿射變換(我們還知道它同時可以表示坐標原點不變的仿射坐標變換)。
正像仿射坐標變換可以分移軸和坐標原點不變的坐標變換兩步來完成—樣，一般的仿射變換也可以分平移和中心仿射變換兩步來完成。這兩個幾何事突不過是同一個代數事實的不同的解釋罷了，從代數上說則是：一般的線性變換都可以分移軸(我們借用這個名詞)和齊次線性變換兩步來完成 。
中心仿射群
仿射幾何是由線性變換群
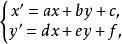中心仿射變換制約的。這種變換可以認為是
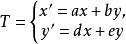中心仿射變換和平移
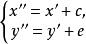中心仿射變換複合而成的。上面像T的這種變換稱為 齊次仿射變換或 中心仿 射變換，這種變換構成的集稱為 齊次仿射群或 中心仿射群。用“中心的"這個形容詞是因為原點或“中心”在這種變換下不變(用x=0，y=0代入即得)。式中a,b,d,e是實參數，並且滿足ae-bd≠0。加上這個條件的原因是：由T的變換公式可以從x和y算出x'和y'，但在ae-bd=0時，這並非克萊因
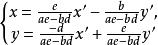中心仿射變換的變換。當ae-bd≠0時，讀者用中學代數中解二元一次方程組的辦法可從T的變換式由x'和y'算出x和y。因而這時T是個變換(一對一的到上映照)。注意，旋轉是一種特殊的仿射變換，此時a=e=cosθ，b=sinθ，d=-sinθ，而ae-bd=cos θ+sin θ=1 。
