概念
仿射等價(affine equivalence)是圖形間的一種等價關係。若存在一個仿射變換把圖形C變成C,則稱C與C仿射等價。否則稱為仿射不等價。圖形的仿射等價是一種等價關係,即具有自反性、對稱性、傳遞性。利用仿射等價關係可以把幾何圖形進行分類。同一類里的圖形具有相同的仿射性質,不同類的兩個圖形間至少存在一個不同的仿射性質。仿射等價的概念在仿射幾何中有廣泛的套用。例如,利用圓和橢圓仿射等價的事實可以得到仿射變換的重要定理:平面上的仿射變換可以分解為一個正交變換和兩個在互相垂直方向上的壓縮(或伸長)的乘積。
仿射變換
由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。
因為正交變換、相似變換、仿射變換都保持共線三點的單比不變,必然保持共線四點的交比不變,所以這些變換都是射影變換。
如果平面上點場的點建立了一個一一對應,並且滿足:
(1)任何共線三點的象仍是共線三點;
(2)共線四點的交比不變。
則這個一一對應叫做點場的射影變換,簡稱射影變換。
仿射幾何
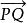 仿射等價
仿射等價幾何學的一個分支學科。主要研究仿射空間中的圖形在仿射對應(仿射變換)下不變的幾何性質和不變數。如共線性、平行性和單比等。n維仿射空間的構成如下:設V是一個n維向量空間,A是一個集合,A中的元素稱為點,如果對於A中兩點P、Q,對應著V中惟一的一個向量,並且這種對應滿足:
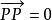 仿射等價
仿射等價1.(V中的零向量)。
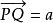 仿射等價
仿射等價2.任給A中一點P和V中的向量a,在A中存在惟一的點Q,使得。
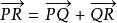 仿射等價
仿射等價3.對A中三點P,Q,R,有等式,則稱A為一個n維仿射空間。特別地,當n=1時稱為仿射直線;n=2時稱為仿射平面;n=3時稱為仿射空間。
在歐幾里得平面(空間)中,若不考慮距離的概念,則這個平面(空間)就是一個仿射平面(空間)。如果在仿射平面(空間)中引進無窮遠點,則這樣的平面(空間)就稱為擴大的仿射平面(空間)。在擴大的仿射平面(空間)中,對原有的點與無窮遠點不加區別,得到的平面(空間)就是射影平面(空間)。仿射幾何中最重要的變換是仿射變換。這種變換的特徵是將共線三點變成共線三點。仿射幾何中最重要的不變數是單比。其他仿射不變數都可以用單比表示。在仿射平面(空間)中,仿射變換的全體構成一個變換群,稱為仿射變換群,簡稱仿射群。並且在擴大的仿射平面(空間)中,它還是保持無窮遠直線(無窮遠平面)不變的一個射影變換群。因此,仿射群是射影群的子群,仿射幾何是射影幾何的子幾何。
正交變換
一類重要的線性變換。設σ是歐氏空間V的線性變換,如果對V的任意向量α,有(σ(α),σ(α))=(α,α),則稱σ是V的正交變換。任意歐氏空間V的線性變換σ是正交變換的充分必要條件是:σ保持向量內積不變,即對V中任意向量α,β,有(σ(α),σ(β))=(α,β)。設V是有限維歐氏空間,σ是V的線性變換,則下列的條件是等價的:
1.σ是正交變換;
2.σ把V的標準正交基變為標準正交基;
3.σ在標準正交基下的矩陣是正交矩陣。
