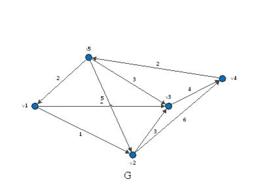
定義
一個郵遞員從郵局出發，要走完他所管轄範圍內的每一條街道，至少一次再返回郵局，如何選擇一條儘可能短的路線？這就是中國郵遞員問題（CPP），其命名是因為中國數學家管梅谷在1962年首先提出了這個問題。如果用頂點表示交叉路口，用邊表示街道，那么郵遞員所管轄的範圍可用一個賦權圖來表示，其中邊的權重表示對應街道的長度。
圖論語言
中國郵遞員問題可用圖論語言敘述為：在一個具有非負權的賦權連通圖G中，找出一條權最小的環遊。這種環遊稱為最優環遊。若G是歐拉圖，則G的任意歐拉環遊都是最優環遊，從而可利用弗勒里算法求解。若G不是歐拉圖，則G的任意一個環遊必定通過某些邊不止一次。將邊e的兩個端點再用一條權為w(e)的新邊連線時，稱邊e為重複的。此時CPP與下述問題等價，若G是給定的有非賦權的賦權連通圖，
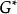中國郵遞員問題
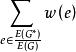中國郵遞員問題（1）用添加重複邊的方法求G的一個歐拉賦權母圖 ，使得 儘可能小；
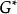中國郵遞員問題（2）求 的歐拉環遊。
此圖圖論中和中國郵遞員問題類似的是旅行商問題，區別於中國郵遞員問題，旅行商問題是說在邊賦權的完全圖中找一個權和最小的哈密爾頓圈。
埃德蒙茲（J.Edmonds）和詹森（E.L.Johnson)在1973年給出了求解（1）的多項式時間算法。
如果郵遞員所通過的街道都是單向道，則對應的圖應為有向圖。1973年，埃德蒙茲和詹森證明此時CPP也有多項式時間算法。帕帕季米特裡屋（C.H.Papadimitrious）在1976年證明，如果既有雙向道，又有單向道，則CPP是NP困難的。
TSP問題
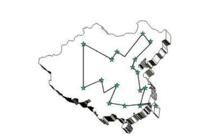中國郵遞員問題Traveling Salesman Problem，即旅行商問題，是數學領域中著名問題之一。假設有一個旅行商人要拜訪N個城市，他必須選擇所要走的路徑，路徑的限制是每個城市只能拜訪一次，而且最後要回到原來出發的城市。路徑的選擇目標是要求得的路徑路程為所有路徑之中的最小值，這是一個NP難問題。
TSP的歷史很久，最早的描述是1759年歐拉研究的騎士週遊問題，即對於西洋棋棋盤中的64個方格，走訪64個方格一次且僅一次，並且最終返回到起始點。
TSP由美國RAND公司於1948年引入，該公司的聲譽以及線形規劃這一新方法的出現使得TSP成為一個知名且流行的問題。
