不可定義性理論
正文
模型論中關於形式語言表達能力的一種研究。在這種研究中，影響較大的有A.帕多瓦、A.塔爾斯基和E.W.貝特等人。可（不可）定義性概念在遞歸論和公理集合論（見集合論）中被廣泛使用，其中有不少特殊的可定義性概念及有關結果，如遞歸論中的分層理論，公理集合論中的可構成集等。設u是形式語言L的一個模型，a是u的一個元素，如果存在L中一個式子嗞(x)，使a是u中唯一的適合嗞(x) 的元素，則稱a為u中的可定義元素，否則稱a為u中的不可定義元素。類似的還可以給出可(不可)定義的函式、集合等概念，它們都可被包含在下述的"可（不可）定義謂詞"概念中。設P(x1,...,xn)是u上的一個謂詞，如果存在L中一個式子嗞(x1,...,xn)，使對u中任何元素a1,...,an都有：P(a1,...,an) 成立若且唯若嗞(x1,...,xn)在u中為真，則稱P(x1,...,xn)為在u上可定義的謂詞；否則稱P（x1,...,xn）為在u上不可定義的謂詞。在一般情況下，並不提出特定的模型u,而是在形式語言中討論可定義性概念。設L是一個形式語言,P和P'是L之外的兩個不同的n元謂詞符號，∑(P)是語言 L∪｛P｝中的一組語句，∑(P')是語言L∪{P'}中相應的語句組。①如果在 ∑(P)∪∑(P')的每一模型中都有 (凬x1,...,xn)【P(x1,...,xn)凮P'(x1,...,xn)】成立，則稱 ∑(P)隱含地定義了謂詞P。②如果存在L中一個式子嗞(x1,...,xn)，使在∑(P)的每一個模型中都有
(凬x1,...,xn)【P(x1,...,xn)凮嗞(x1,...,xn)】成立，則稱∑(P)明顯地定義了謂詞P。
由以上定義可以看出，如果∑(P)明顯地定義P，則它也隱含地定義P。所以，如果要說明某一組語句∑(P)不能明顯地定義P，只需說明 ∑(P)不能隱含地定義P就夠了，換句話也就是說，只需找到∑(P)∪∑(P')的一個模型,在其中P與P'有不同的解釋就夠了。這一方法稱為帕多瓦方法。在這方面，貝特在帕多瓦和塔爾斯基的工作基礎上進一步證明了：∑(P)隱含地定義P若且唯若∑(P)明顯地定義P。從而表明,如果∑(P)不能明顯地定義P，則這種不可定義性必能用帕多瓦方法來說明。
在具體模型中的不可定義性方面，塔爾斯基有一個關於自然數系統中真語句集不可定義性的著名定理，其內容如下:令語言 L={+,·,S,O},取L的模型
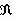=(N,+,·,S,O),其中 N為自然數集,S為"後繼"運算，考慮L中一切在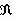中為真的語句的集合T,通過適當的有效編碼 ,就可以把 T看作N的子集。塔爾斯基定理是說：T是不可定義的。該定理與關於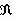的判定問題的不可解性有一定聯繫。 80年代以來，在模型論中對於模型的範疇性，也就是它的完備理論的範疇性，有較多的研究，從性質上說，這是一種關於可定義性的廣義研究。例如，有理數域不是埲 -範疇的，其含義是：在可數無限域範圍內，有理數域不能用關於它的一切一階真語句所成的集合唯一地刻劃；又如，複數域是埌 -範疇的，其含義是：在基數為埌的無限域範圍內，複數域可以用關於它的一切一階真語句所成的集合唯一地刻劃。
