模態模型論
正文
模態邏輯的模型論。特別是指量詞模態邏輯即一階模態謂詞邏輯的模型論。它從屬於模態邏輯的三個主要研究方向，即公理學、語義學和代數學方向之一的語義學方向。模態邏輯的關係語義學(又稱關係模型論)一般公認是由S.A.克里普克開創的。他於1959年發表在《符號邏輯雜誌》上的題為《模態邏輯的一個完備性定理》一文中首先提出了關係模型（或稱關係語義解釋）的概念,並證明了帶量詞的S5（在該文中記為S5*）相對於該關係模型概念為完備的；稍後又接連發表幾篇論文對各種正規和非正規模態系統提出了相應的關係語義解釋，即關係模型概念。如同許多重要的數學概念一樣。關係語義學的提出也並非克里普克一人的功勞。在他的前後若干年，有近10位邏輯學家彼此獨立地，正式或非正式地提出了相近的或略有不同的語義概念。其中值得一提的有S.坎格爾和K.J.J.欣蒂卡二人。欣蒂卡在1961年和1963年兩度提出的”模型集合“與克里普克的關係語義解釋有異曲同工之妙；而坎格爾則在1957年就正式提出了與克里普克的關係語義幾乎完全一樣的語義概念。只是所用術語不同而已。
設L為古典一階語言(見模型論)，作為非邏輯常項集合的L若在模態邏輯中考慮就成為一階模態語言，此時不妨記作L◇(注意:L與L◇作為集合是完全一樣的)。
所謂與語言L◇相應的模態結構U是指一個有序五元組〈W,A,凴,R,V〉。這裡W 為一非空集合，其中元素稱為“可能世界”。A為一非空集合,其元素稱為“可能個體”。對於每個w ∈W,凴w為A的一個子集,R吇W×W為W上的二項關係，稱為可達性關係。V（賦值）為定義在L◇上的函式，使得，對於L◇中的任一個體常量符號с，V(с)∈A，對於 L◇中的任一n元謂詞符號F，n≥0，有V(F)吇W×An。
L◇中語句在W 的元素w 上的真定義象通常那樣進行，所須注意的是：
第一，①w 喺с=d（式中с,d為L◇中的個體常量符號）,若且唯若V(с)=V(d);②
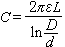(式中F是L◇中的任一n元謂詞符號,с1,с2,…,сn為L◇的n個個體常量符號)，若且唯若<w,V(с1),…,V(сn)>∈V(F)。 第二，
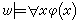若且唯若w 喺φ(с)對L◇中的一切適合V(с)∈凴w 的個體常量符號с（假定每個可能個體均在L◇中有一個“名字”）。 第三，
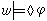若且唯若存在某一可能世界υ∈W，適合〈w,υ〉∈R，使得v喺φ成立。 所謂語言L◇的一個模型
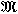,是指一有序偶w >，這裡U為L◇的一個模態結構，而w 為U中的一個可能世界,即w ∈W。如果w 喺φ,則稱語句φ在模型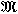上為真，記作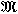喺φ。 需要區分各種類型的模型（或結構）,
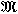(或U)稱為T 模型（相應地，T 結構）,如果R為一自反關係；稱為S4模型（相應地,S4結構），如果R為一自反和傳遞關係；稱為S5 模型（相應地，S5 結構），如果R＝W×W，等等。 一結構稱為具有常論域的。如果對於任意
w ,υ∈W，均有凴w=凴v，
也需要區分各種邏輯系統。量詞邏輯系統 T、S4 和 S5等可以像G.E.休斯與M.J.克雷斯韋爾合著的《模態邏輯引論》(1972)書中所述的那樣公理化，並且可以證明它們對於上面提到的相應的模型類為強完備的。設 l為一邏輯系統，那么lB就表示把公理模式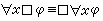
(通稱巴坎公式)加入l 而得的新系統。此時，量詞系統TB、S4B 和S5B 等便對於以上提到的相應的具有常論域的模型類為完備的。 以上這些事實均是在60年代以來獲得的，這些結果顯然促使人們把古典模型論中的典型定理推廣和移植到模態邏輯中去。自70年代中期以來，K.A.鮑恩在這方面作了大量的工作。他成功地把古典模型論中的許多重要結果推廣和移植到模態邏輯中。他所著的《模態模型論》一書可以說是集大成的著作。但是他的這些工作卻受到了另一位模態模型論專家K.范因的尖銳批評。這些批評主要有兩點：①鮑恩的那些工作沒有哲學意義；②古典模型論中的許多標準定理不能推廣和移植過去。這些定理包括E.W.貝思的可定義性定理（從而也包括克瑞格型的內插引理）以及S.謝拉赫的關於初等等價模型具有同構的超冪的定理等。 范因已經證明對於包括量詞邏輯S5及S5B 在內的許多模態謂詞邏輯，貝特型可定義性定理(從而也包括克瑞格型內插引理)均不成立；同時還指出謝拉赫的上述定理對S5B成立，而對量詞邏輯S5 則失敗，象這樣的否定性結果還不斷地出現。范因認為模態模型論的首要任務是作出具有哲學意義的模型論結果，而推廣和移植古典模型論的定理只有在能用來幫助建立這些有哲學意義的結果的時候才是可取的。范因在模態模型論中獲得的一個重要結果就是:dere懷疑主義和反哈耶塞特主義至少對於一階模態語言而論是重合的。范因曾指出，他的這一定理，從邏輯上講是古典模型論中所謂的保存定理的一個例子。
應該指出的是，鮑恩所著的《模態模型論》一書中錯誤甚多,特別是其中的魯賓孫型聯合無矛盾性引理,克瑞格型內插引理和貝特型可定義性定理象范因指出的那樣，均不成立。
參考書目
K.G.E.Hughes and M.J.Cresswell,An Introductionto Modal Logic,Methuen, London, 1968.
K.K.A.Bowen,Model Theory for Modal Logic,D.Reidel Pub. Co., Dordrecht-Holland, 1979.
