三面角

三面角是指由三個面構成的多面角，可記作為∠O-ABC。

定義

由三個面構成的多面角稱為三面角，如圖中三面角可記作∠O-ABC。
特別地，三個面角都是直角的三面角稱為直三面角。

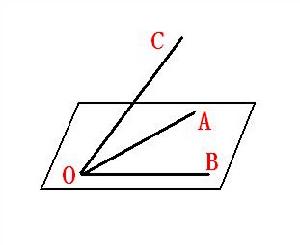三面角

性質

1、三面角的任意兩個面角的和大於第三個面角。
2、三面角的三個二面角的和大於180°，小於540°。

三面角相關定理

設三面角∠O-ABC的三個面角∠AOB、∠BOC、∠AOC所對的二面角依次為∠OC，∠OA，∠OB。
1、三面角正弦定理：
sin∠OA/sin∠BOC=sin∠OB/sin∠AOC=sin∠OC/sin∠AOB。
證明過程如下：

三面角正弦定理

2、三面角第一餘弦定理：
cos∠BOC=cos∠OA×sin∠AOB×sin∠AOC+cos∠AOB×cos∠AOC。
證明過程如下：

三面角餘弦定理證明

3、三面角第二餘弦定理：
cos∠OA=cos∠BOC×sin∠OB×sin∠OC-cos∠OB×cos∠OC。
從三面角第一餘弦定理中消去∠AOB和∠AOC即可得