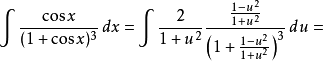三角換元法

含有的積分在積分中，我們可以用以下的代換：這樣積分變為：注意以上的步驟需要 例如，當''x''從0增加到''a''/2時，sin 因此，我們有：含有的積分在積分中，我們可以用以下的代換：這樣，積分變為：（''a''

三角換元法三角換元法是一種計算積分的方法，是換元積分法的一個特例。
含有a^2-x^2的積分
在積分\int\frac{dx}{\sqrt{a^2-x^2}}中，我們可以用以下的代換：
x=a\sin(\theta),\ dx=a\cos(\theta)\,d\theta
\theta=\arcsin\left(\frac{x}{a}\right)
這樣積分變為：
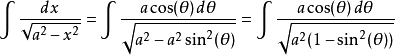
\int\frac{dx}{\sqrt{a^2-x^2}} = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2-a^2\sin^2(\theta)}} = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2(1-\sin^2(\theta))}}
{} = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2\cos^2(\theta)}} = \int d\theta=\theta+C=\arcsin\left(\frac{x}{a}\right)+C
注意以上的步驟需要 a > 0和cos(θ) > 0；我們可以選擇a為a2的算術平方根，然後用[[反正弦]]函式把''θ''限制為−π/2 < ''θ'' < π/2。
對於定積分的計算，我們必須知道積分限是怎樣變化。例如，當''x''從0增加到''a''/2時，sin(θ)從0增加到1/2，所以θ從0增加到π/6。因此，我們有：
\int_0^{a/2}\frac{dx}{\sqrt{a^2-x^2}}=\int_0^{\pi/6}d\theta=\frac{\pi}{6}.含有a^2+x^2的積分
在積分\int\frac{dx}{a^2+x^2}中，我們可以用以下的代換：
x=a\tan(\theta),\ dx=a\sec^2(\theta)\,d\theta
\theta=\arctan\left(\frac{x}{a}\right)
這樣，積分變為：
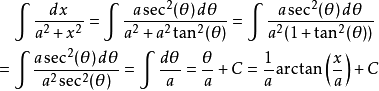\begin{align}& {} \quad \int\frac{dx}{a^2+x^2} = \int\frac{a\sec^2(\theta)\,d\theta}{a^2+a^2\tan^2(\theta)} = \int\frac{a\sec^2(\theta)\,d\theta}{a^2(1+\tan^2(\theta))} \\& {} = \int \frac{a\sec^2(\theta)\,d\theta}{a^2\sec^2(\theta)} = \int \frac{d\theta}{a} = \frac{\theta}{a}+C = \frac{1}{a} \arctan \left(\frac{x}{a}\right)+C\end{align}（''a'' > 0）。
含有x^2-a^2的積分
在積分\int\frac{dx}{x^2 - a^2}中，可以用部分公式的方法來計算，但是，
\int\sqrt{x^2 - a^2}\,dx
則必須要用換元法：
x = a \sec(\theta),\ dx = a \sec(\theta)\tan(\theta)\,d\theta
\theta = \arcsec\left(\frac{x}{a}\right)
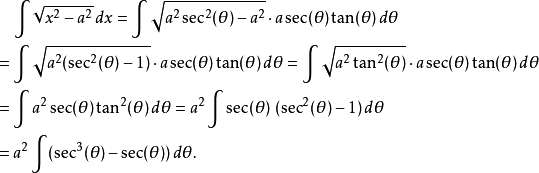
\begin{align}& {} \quad \int\sqrt{x^2 - a^2}\,dx = \int\sqrt{a^2 \sec^2(\theta) - a^2} \cdot a \sec(\theta)\tan(\theta)\,d\theta \\& {} = \int\sqrt{a^2 (\sec^2(\theta) - 1)} \cdot a \sec(\theta)\tan(\theta)\,d\theta = \int\sqrt{a^2 \tan^2(\theta)} \cdot a \sec(\theta)\tan(\theta)\,d\theta \\& {} = \int a^2 \sec(\theta)\tan^2(\theta)\,d\theta = a^2 \int \sec(\theta)\ (\sec^2(\theta) - 1)\,d\theta \\& {} = a^2 \int (\sec^3(\theta) - \sec(\theta))\,d\theta.\end{align}
含有三角函式的積分
對於含有三角函式的積分，可以用一下的代換：
\int f(\sin x,\cos x)\,dx=\int\frac1{\pm\sqrt{1-u^2}}f\left(u,\pm\sqrt{1-u^2}\right)\,du, \qquad \qquad u=\sin x
\int f(\sin x,\cos x)\,dx=\int\frac{-1}{\pm\sqrt{1-u^2}}f\left(\pm\sqrt{1-u^2},u\right)\,du \qquad \qquad u=\cos x
\int f(\sin x,\cos x)\,dx=\int\frac2{1+u^2} f\left(\frac{2u}{1+u^2},\frac{1-u^2}{1+u^2}\right)\,du \qquad \qquad u=\tan\frac x2
\int\frac{\cos x}{(1+\cos x)^3}\,dx = \int\frac2{1+u^2}\frac{\frac{1-u^2}{1+u^2}}{\left(1+\frac{1-u^2}{1+u^2}\right)^3}\,du =
\frac{1}{4}\int(1-u^4)\,du = \frac{1}{4}\left(u-\frac15u^5\right) + C = \frac{(1+3\cos x+\cos^2x)\sin x}{5(1+\cos x)^3} + C

相關詞條

相關搜尋

熱門詞條

聯絡我們