基本介紹
下三角形行列式
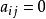三角形行列式主對角線上方元素全為零的行列式，也即非零元素只出現在主對角線及下方的行列式，稱為 下三角形行列式(當i<j時， )。
對下三角形行列式總有：
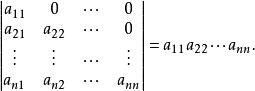三角形行列式證明：行列式及其餘子式均依次按第一行展開即得 。
上三角形行列式
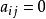三角形行列式主對角線下方元素全為零的行列式，也即非零元素只出現在主對角線及上方的行列式，稱為上三角形行列式(當i>j時， )。
對上三角形行列式也總有：
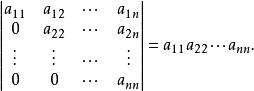三角形行列式證明：行列式及其餘子式均依次按第一行展開即得(或因為上三角形行列式與下三角形行列式互為轉置行列式) 。
對角形行列式
主對角形行列式：主對角線上方、下方的元素全為零的行列式稱為主對角形行列式。
主對角形行列式既是上三角形行列式又是下三角形行列式。
副對角形行列式：副對角線上方、下方的元素全為零的行列式稱為副對角形行列式。
化為上(下)三角形行列式
在計算行列式(特別是數字行列式)時，可先利用 行列式的性質，把行列式化為上(下)三角形行列式，再利用上面的結果進行計算 。
解題思路：利用行列式的性質，可逐步將所給行列式化為三角形行列式，化零時一般儘量選含有1的行(列)及含零較多的行(列)，若沒有1，則可適當選取便於化為零的數，或利用行列式的性質將某行(列)中的某數化為1；若所給行列式中元素間具有某些特徵，則應充分利用這些特徵，常見的有：
(1)行列式所有行(或列)全部元素化為1；
(2)對爪形(三線型)行列式，可通過將其餘各行(或列)的某一倍數加到第1行(或列)而化為三角形行列式；
(3)若行列式的各行(或列)之間差別不大，可採用逐行(或列)相加(或減)的方法，將其化簡後進行計算；
(4)對某些行列式，可在原行列式中增加一行一列，且保持原行列式不變，使其具有某種特徵，便於計算，一般稱此法為加邊法；
總之，掌握 行列式的特徵是計算行列式的關鍵，在此基礎上，充分利用行列式的性質，靈活選用方法，值得注意的是，同一個行列式有時會有不同的求解方法，可選取相對簡單的方法或自己最熟悉的方法 。
【例1】計算行列式：
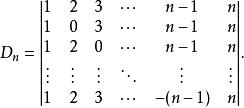三角形行列式解：將第一行分別加到第2,3,4,...,n行，有
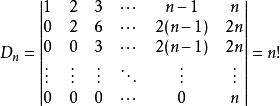三角形行列式【例2】計算行列式：
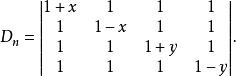三角形行列式解：將第2行乘-1加到第1行，再第4行乘-1加到第3行，分別有
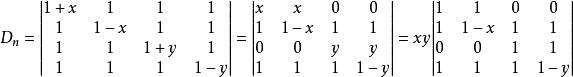三角形行列式
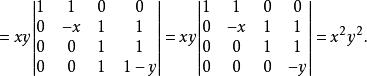三角形行列式