三角形內心

三角形內心，在三角形中，三個內角的三條角平分線的相交於一點，這個點叫做三角形的內心。這個點也是這個三角形內切圓的圓心。三角形內心到三角形三條邊的距離相等。做出△ABC的兩個內角的平分線，交於一點，該點即為三角形內心。做出△ABC的外接圓O，過圓心O分別作AC、BC（任意兩邊）的垂線，兩條垂線與圓O交於E、F，連線AF、BE交於點I，則點I即為內心。內切圓的半徑。（1）在RtΔABC中，∠C=90°，r=(a+b-c)/2，（2）在RtΔABC中，∠C=90°，r=ab/(a+b+c)，（3）任意△ABC中r=（2*S△ABC）/C△ABC （C為周長）。

基本信息

• 中文名：三角形內心

• 套用領域：幾何
• 性質：內心到三角形三條邊的距離相等
• 定義：三條角平分線的交點

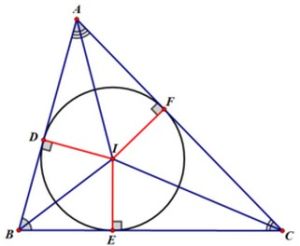
共點證明

證明：如圖所示
作∠B、∠C角分線與AC、AB交與F、D
CD與BF交與I連線AI交BC於E
由塞瓦定理有（AD/BD）*（BE/CE）*（CF/AF）=1
∵BF、CD為角分線
∴由角分線定理有AD/BD=AC/BC CF/AF=BC/AB
∴BE/CE=AB/AC
由角平分線定理的逆定理有AE為∠A的角分線
證畢

內心性質

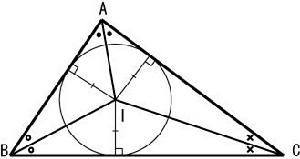三角形內心

設△ABC的內切圓為☉I(r)，角A、B、C的對邊分別為a、b、c，p=(a+b+c)/2．
1、三角形的內心到三邊的距離相等，都等於內切圓半徑r．
2、∠BIC=90°+A/2．
3、如圖 在RT△ABC中，∠A=90°△內切圓切BC於D則S△ABC=BD*CD4、點O是平面ABC上任意一點，點I是△ABC內心的充要條件是：向量OI=[a(向量OA)+b(向量OB)+c(向量OC)]/(a+b+c)．
5、△ABC中，A(x1，y1)，B(x2，y2)，C(x3，y3)，那么△ABC內心I的坐標是：(ax1/(a+b+c)+bx2/(a+b+c)+cx3/(a+b+c)，ay1/(a+b+c)+by2/(a+b+c)+cy3/(a+b+c))．
6、(歐拉定理)⊿ABC中，R和r分別為外接圓為和內切圓的半徑，O和I分別為其外心和內心，則OI^2=R^2-2Rr．
7、點O是平面ABC上任意一點，點I是△ABC內心的充要條件是：a(向量OA)+b(向量OB)+c(向量OC)=向量0．
8、　雙曲線上任一支上一點與兩焦點組成的三角形的內心在實軸的射影為對應支的頂點。
9、△ABC中，內切圓分別與AB，BC，CA相切於P，Q，R，則AP=AR=（b+c-a）/2，BP =BQ =(a+c-b)/2,CR =CQ =(b+a-c)/2,r=[(b+c-a)tan(A/2)]/2。
10、（內角平分線定理）
△ABC中，0為內心，∠A 、∠B、 ∠C的內角平分線分別交BC、AC、AB於Q、P、R，則BQ/QC=c/b, CP/PA=a/c, BR/RA=a/b.