三角函式萬能公式

三角函式萬能公式為：(1)(sinα)^2+(cosα)^2=1，(2)1+(tanα)^2=(secα)^2，(3)1+(cotα)^2=(cscα)^2；證明下面兩式，只需將一式，左右同除(sinα)^2，第二個除(cosα)^2即可；(4)對於任意非直角三角形，總有tanA+tanB+tanC=tanAtanBtanC。

基本信息

• 中文名：三角函式萬能公式

• 套用領域：數學

萬能公式

證明

三角函式萬能公式

三角函式萬能公式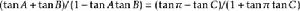

三角函式萬能公式

整理可得

三角函式萬能公式

得證

同樣可以得證,當x+y+z=nπ(n∈Z)時,該關係式也成立

由tanA+tanB+tanC=tanAtanBtanC可得出以下結論

(5)cotAcotB+cotAcotC+cotBcotC=1

(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)

(7)(cosA）^2+(cosB）^2+(cosC）^2=1-2cosAcosBcosC

證明

由餘弦定理：a^2+b^2-c^2-2abcosC=0

正弦定理：a/sinA=b/sinB=c/sinC=2R

得 （sinA）^2+（sinB）^2-（sinC）^2-2sinAsinBcosC=0

轉化 1-(cosA）^2+1-(cosB）^2-[1-(cosC）^2]-2sinAsinBcosC=0

即 (cosA）^2+(cosB）^2-(cosC）^2+2sinAsinBcosC-1=0

又 cos（C）=-cos(A+B)=sinAsinB-cosAcosB

得 (cosA）^2+(cosB）^2-(cosC）^2+2cosC[cos（C）+cosAcosB]-1=0

(cosA）^2+(cosB）^2+(cosC）^2=1-2cosAcosBcosC

得證

(8)（sinA）^2+（sinB）^2+（sinC）^2=2+2cosAcosBcosC

函式公式

設tan(A/2)=t

sinA=2t/(1+t^2) （A≠2kπ+π，k∈Z）

tanA=2t/(1-t^2) （A≠2kπ+π，k∈Z）

cosA=(1-t^2)/(1+t^2) （A≠2kπ+π k∈Z）

就是說sinA.tanA.cosA都可以用tan(A/2)來表示,當要求一串函式式最值的時候,就可以用萬能公式，推導成只含有一個變數的函式，最值就很好求了。