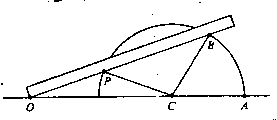三等分角問題

三等分角問題（trisection of an angle）是二千四百年前，古希臘人提出的幾何三大作圖問題之一，即 用圓規與直尺把一任意角三等分。問題的難處在於作圖使用工具的限制。古希臘人要求
幾何作圖只許使用直尺 （沒有刻度，只能作直線的尺）和圓規。這問題曾吸引著許多人去研究，但
都無一成功。１８３７年凡齊爾（ １８１４－１８４８）運用代數方法證明了，這是一個標尺作圖
的不可能問題。
在研究「三等分角」的過程中發現了如蚌線、心臟線、圓錐曲線等特殊曲線。人們還發現，只
要放棄「尺 規作圖」的戒律，三等分角並不是一個很難的問題。古希臘數學家阿基米德（前２８７
－前２１２）發現只要 在直尺上固定一點，問題就可解決了。現簡介其法如下：在直尺邊緣上添加
一點Ｐ，命尺端為Ｏ。
設所要三等分的角是∠ＡＣＢ，以Ｃ為圓心，CＰ為半徑作半圓交
角邊於Ａ，Ｂ；使Ｏ點在ＣＡ延線上移 動，Ｐ點在圓周上移動，當尺通過Ｂ時，聯ＯＰＢ（見圖）
。由於ＯＰ＝ＰＣ＝ＣＢ，所以∠ＣＯＢ＝∠ＡＣ Ｂ／３。這裡使用的工具已不限於標尺，而且作
圖方法也與公設不合。

需要注意的是，世間萬物都有無窮無盡的變化，誰都不知道將來會不會解決這個問題，所以如果思維到了一個新的境界，可能在這個問題上會有進展，這就靠下一代的努力了。