【說明】：此教學設計任務由南京曉莊學院現代教育技術課程老師yqiong參與教師-維基星光計畫進行wiki教學而發布。此詞條為範例詞條，由陳珊珊選定主題並負責、參與現代教育技術課程的所有同學協作共同完成！
基本信息
科目：數字系統 教學對象：大學一年級計算機系的學生課時：4課時 教學環境：多媒體教室
學習者特徵分析
本節課的教學對象是大學一年級計算機系的學生，他們思維能力強，能獨立的學習和思考，能很好的接受新知識 。由於十進制的數字在他們的腦海里已經根深蒂固，所以要有一段時間接受二進制，八進制，十六進制，期間要不斷強化二進制，八進制和十六進制系統，否則，在進行“設計算法”、“編寫程式”環節教學，會存在一定困難，難以深入開展下去。
學習內容分析
《數字系統》選自機械工業出版社出版的《計算機科學導論》 ，本章是第3.4章的先導。在第3章中將要說明數據是如何存儲在計算機中的。在第四章中將要講解邏輯運算和算術運算是如何作用於數據的。本章將說明十進制系統，二進制系統，八進制系統，十六進制系統，以及它們之間的轉換和非位置化數字系統。要了解計算機，首先要了解計算機中數的表示方法。
教學目標分析
知識與技能
1.準確說出數字系統的定義；
2.能準確說出非位置化和位置化數字系統的區別；
3.準確說出十進制系統，二進制系統，八進制系統，十六進制系統的含義；
4．能準確的將二進制，八進制，十六進制數字轉換成十進制系統；
5.能準確的將十進制數字轉換成二進制，八進制，十六進制系統；
6.能準確的將二進制和八進制數字相互轉換；
7.能準確的將二進制和十六進制數字相互轉換。
過程和方法
通過任務引導學生經歷分析問題、解決問題，實踐練習、提出問題，解決問題，課後交流等解決問題的過程，讓學生初步了解四種不同進制，然後再進一步掌握四種不同進制的轉換。
情感態度與價值觀
學習的知識與以前的知識有很大的不同，能使學生有成就感，能激發學生的求知慾。
教學重點與難點
重點
位置化數字系統和非位置化數字系統的不同。
四種不同進制之間的轉換。
難點
十進制數整數部分和小數部分轉換到其它與其等值底的過程。
教學策略的選擇與設計
本節課主要採用了講授法，自主探究學習方法，任務驅動法，強化練習法，交流討論法等。從課前思考題入手，快速自然的引導學生走進主題，明確本節課的學習目標，引發學生積極思考；講授新課內容，以醒目的方式將四種進制之間的轉換過程呈現給學生；進行課堂交流，充分挖掘學生潛力，讓學生在交流討論中近一步了解四種進制。在結束環節，以課後作業強化練習法結束本節課，使學生對四種進制的轉換的暫時記憶轉化為長期記憶。
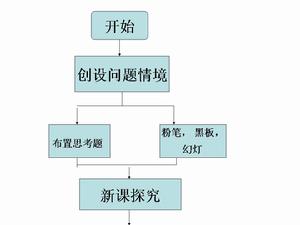教學流程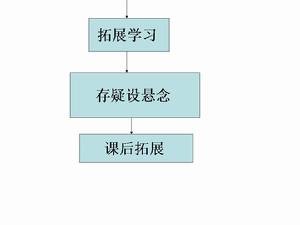
教學流程
教學流程教學設計
創設問題情境
1.教師活動：布置思考題（101+ 1=110 ？對or錯），思考在日常生活中，四種進制在哪些 地方比較常見？準備上課資源。
2.學生活動：
課前複習，認真思考老師布置的思考題並積極思考在什麼情況下 101+1=110是正確的。思考在日常生活中，四種進制在哪些地方比較常見？
3.設計意圖：
促使學生課前複習，激發學生的求知慾。
4.媒體及資源準備:
課本後的練習題，圖書館裡關於數字系統的資料，計算機
新課探究1.教師活動：
教師講解思考題（1011=110？對or錯）， 在十進置系統中，這等式是錯誤的，但在二進置系統中，它卻是正確的。
導入課題：描述位置化數字系統，十進制系統，二進制系統，八進制系統，十六進制系統，非位置化數字系統。
十進制：
十進制數是日常生活中使用最廣的計數制 。組成十進制數的符號有0，1，2，3，4， 5，6，7，8，9等共十個符號，我們稱這些符號為數碼。在十進制中，每一位有
0～9共十個數碼，所以計數的基數為10。 超過9就必須用多位數來表示。十進制數的運算遵循：加法時：“逢十進一”； 減法時：“借一當十”。
（1）十進制轉換為二進制，分為整數部分和小數部分
1.整數部分方法：除2取余法，即每次將整數部分除以2，餘數為該位權上的數，而商繼續除以2，餘數又為上一個位權上的數，這個步驟一直持續下去， 直到商為0為止，最後讀數時候，從最後一個餘數讀起，一直到最前面的一個餘數。
下面舉例：
例：將十進制的168轉換為二進制得出結果。
分析：
第一步，將168除以2,商84,餘數為0。
第二步，將商84除以2，商42餘數為0。
第三步，將商42除以2，商21餘數為0。
第四步，將商21除以2，商10餘數為1。
第五步，將商10除以2，商5餘數為0。
第六步，將商5除以2，商2餘數為1。
第七步，將商2除以2，商1餘數為0。
第八步，將商1除以2，商0餘數為1。
第九步，讀數，因為最後一位是經過 多次除以2才得到的，因此它是最高位，
讀數字從最後的餘數向前讀，即10101000
2.小數部分方法：乘2取整法，即將小數部分乘以2，然後取整數部分，剩下的小數部分繼續乘以2，然後取整數部分，剩下的小數部分又乘以2，一直取到小數...
二進制：
電子計算機處理的信息，都是僅用“0” 與“1”兩個簡單數字表示的信息，或者是用這種數字進行了編碼的信息。這種數制叫做二進制。二進制計算法的特點 ：①二進制數只有“0”和“1”兩個數碼， 基數是2，最大的數字是1； ②採用逢二進一的原則。
二進制的優點是：
■二進制只有“0”和“1”兩數字，很容易表示。電壓的高和低、電晶體的截止與飽和、磁性材料的磁化方向等都可 以表示為“0”和“1”兩種狀態。
■二進制數的每一位只有0和1兩狀態, 只需要兩種設備就能表示,所以二進制數節省設備。由於狀態簡單，所以抗干擾力強，可靠性高。
二進制轉換成十進制 ：
二進制數第0位的權值是2的0次方，第1位的權值是2的1次方…… 所以，設有一個二進制數：01100100，轉換為10進制為：
下面是豎式：
01100100換算成十進制
第0位0*20=0
第1位0*21=0
第2位1*22=4
第3位0*23=0
第4位0*24=0
第5位1*25=32
第6位1*26=64
第7位0*27=0＋
---------------------------
100
用橫式計算為：
0*20+0*21+1*22+1*23+ 0*24+1*25+1*26+0*27=100
0乘以多少都是0，所以我們也可以直接跳過值為0的位：
1*22+1*23+1*25+1*26=100
八進制：
八進制就是逢8進1。 八進制數採用0～7這八數來表達一個數。 八進制數第0位的權值為8的0次方，第1 位權值為8的1次方，第2位權值為8的2次方……
所以，設有一個八進制數：1507，轉換為十進制為：
用豎式表示：
1507換算成十進制。
第0位7*80=7
第1位0*81=0
第2位5*82=320
第3位1*83=512＋
--------------------------
839
同樣，我們也可以用橫式直接計算：
7*80+0*81+5*82+1*83=839
結果是，八進制數1507轉換成十進制數為839 。
一個數如果要指明它採用八進制，必須在它前面加上一個0，如：123是十進制， 但0123則表示採用八進制。
十六進制：
16進制就是逢16進1，但我們只有0~9這 十個數字，所以我們用A，B，C，D，E， F這五個字母來分別表示10，11，12，13， 14，15。字母不區分大小寫。
十六進制數的第0位的權值為16的0次方，第1位的權值為16的1次方，第2位的權值 為16的2次方…… 所以，在第N（N從0開始）位上，如果是數X（X大於等於0，並且X小於等於15， 即：F）表示的大小為X*16的N次方。
假設有一個十六進數2AF5,那么如何
換算成10進制呢？
用豎式計算：
2AF5換算成10進制:
第0位：5*160=5
第1位：F*161=240
第2位：A*162=2560
第3位：2*163=8192＋
-------------------------------------
10997
直接計算就是：
5*160+F*161+A*162+2*163=10997
(別忘了，在上面的計算中，A表示10，而F表示15)
16進制數必須以0x開頭。
十進制轉換成二進制 ：
10進制數轉換成二進制數，這是一個連續除2的過程：把要轉換的數，除以2，得到商和餘數，將商繼續除以2，直到商為0。最後將所有餘數倒序排列，得到數就是轉換結果。
聽起來有些糊塗？我們結合例子來說明。
比如要轉換6為二進制數
轉換6為二進制
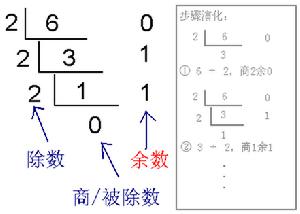轉換6為二進制2.學生活動：
進入學習情景；聽老師的講述並積極思考，認真領會不同進制之間的轉換。
完成下列題目：
1.以下哪種表示法是錯誤的？
A.(10111)2B.(349)8
C.(3AB)16D.256
2.以下哪個數與十進制數12等值？
A.(1110)2B.(C)16
C.(15)8D.以上都不對
3.將下列二進制數轉換成十進制數。
a.(01101)2
b.(1011000)2
4.將下列十六進制轉換成十進制。
a.(AB2)16
b.(123)16
5.將下列八進制數轉換成十進制。
a.(237)8
b.(2731)8
6將下列十進制數轉換成二進制。
a.1234
b.14.56
3.設計意圖：
1.利用學生的好奇心來使學生認真聽講。
2.利用習題使學生能理解四種不同的進制及其轉換。
4.媒體及資源準備：
粉筆， 黑板， 幻燈
拓展學習：1.教師活動：
讓學生自己摸索如何把十進制轉換成八進制和十六進制。
2.學生活動：
熟悉掌握十進制轉換成二進制的方法，思考如何把十進制轉換成八進制和十六進制。
將下列十進制轉換成八進制：
a.1156
b.99
將下列十進制轉換成十六進制：
a.567
b.1411
3.設計意圖：
使學生自主學習。
4.媒體及資源準備：
黑板，粉筆
存疑設懸念
1.教師活動：
二進制怎么轉換成十六進制？ 有沒有捷徑呢？
首先我們來看一個二進制數：1111， 它是多少呢？
你可能還要這樣計算：1*20+1*21 +1*22+1*23=1*1+1*2+1*4+1*8=15。
然而，由於1111才4位，所以我們必須直接記住 它每一位的權值，並且是從高位往低位記， 8、4、2、1。即，最高位的權值為23＝8， 然後依次是22＝4，21＝2，20＝1。
記住8421，對於任意一個4位的二進制數， 我們都可以很快算出它對應的10進制值。
下面列出四位二進制數xxxx所有可能的值（中間略過部分）
僅4位的2進制數快速計算方法十進制值十六進值
1111 =8+4+2+1=15 F
1110 =8+4+2+0=14 E
1101 =8+4+0+1=13 D
1100 =8+4+0+0=12C
1011 =8+4+0+1=11 B
1010 =8+0+2+0=10 A
1001 =8+0+0+1=10 9
....
0001 =0+0+0+1=1 1
0000=0+0+0+0=0 0
二進制數要轉換為十六進制，就是以4位一段，分別轉換為十六進制。
如(上行為二制數，下面為對應的十六進制)：
1111，1101，1010，0101，1001，1011
F，D，A，5，9，B
反過來，當我們看到FD時，如何迅速將 它轉換為二進制數呢？
先轉換F：
看到F，我們需知道它是15（可能你還不熟悉 A～F這五個數），然後15如何用8421湊呢？ 應該是8+4+2+1，所以四位全為1：1111。
接著轉換D：
看到D，知道它是13，13如何用8421湊呢？ 應該是：8+2+1,即：1011。 所以,FD轉換為二進制數，為：11111011
由於十六進制轉換成二進制相當直接， 所以，我們需要將一個十進制數轉換 成2進制數時，也可以先轉換成16進制， 然後再轉換成2進制。
比如，十進制數1234轉換成二制數， 如果要一直除以2，直接得到2進制數 ，需要計算較多次數。所以我們可以先 除以16，得到16進制數:
被除數計算過程商 餘數
12341234/16772
7777/16413(D)
44/16 0 4
結果16進制為：0x4D2
然後我們可直接寫出0x4D2的二進
制形式：010010110010。
其中對映關係為：
0100--4
1011--D
0010--2
同樣，如果一個二進制數很長，我們需要將它轉換成10進制數時，除了前面學過的方法是，我們還可以先將這個二進制轉換成16進制，然後再轉換為10進制。
下面舉例一個int類型的二進制數：
01101101111001011010111100011011
我們按四位一組轉換為16進制：6D E5 AF 1B
2.學生活動：
將下列二進制轉換成十六進制：
a.(10110011)2
b.(11110111)2
3.設計意圖：
調動學生積極思考。
4.媒體及資源準備：
計算機， 幻燈
1.教師活動：
布置課後習題，提供學習資源。
2.學生活動：
積極完成作業，自己另外再找一些題目練習。
3.設計意圖：
鞏固學習知識，使短暫記憶轉換成長期記憶。
4.媒體及資源準備：
計算機，幻燈，粉筆
教學評價
從以下幾個方面來考查學生的學習情況，並將學生學習的評價融入各個教學活動過程中。
（1）課前認真預習
（2）課堂表現較好，認真聽老師的講解，積極舉手回答問題，參與面較廣
（3）熟練的進行十進制，二進制，八進制，十六進制的轉換。
（4）課後練習題準確率高
（5）課後認真閱讀書後的“推薦閱讀”。
1、學生自評表：
知識評價： 是否知道了什麼是十進制，二進制，八進制，十六進制； 是否能準確進行四種不同進制之間的轉換；
學生課堂表現評價： 認真、積極、自信、善於與人討論、思維的有條理
能力評價：這節課我能拿個“----”（A、B、C、D）。
2、教師評價：
A（優秀）
學生能課前認真預習，上課認真聽講。
課堂表現良好，積極回答問題，參與面廣，投入課堂交流。
B（良好）
學生上課認真聽講，課堂表現良好，積極回答問題，能完成大部分課後練習。
C（及格）
學生課堂表現良好，能完成少部分課後練習。
備註與反思
本課時從課前的思考題出發，通過講授法、自主探究、課堂交流學習法等，讓學生經歷分析問題，解決問題，實踐練習，提出問題，解決問題，課後交流過程，學習四種不同的數字系統。設定的問題新穎，能激發學生的好奇心和求知慾。
在教學的實施過程中要注重個體差異，學生對數字的敏感程度不一樣，接收能力也會不一樣，對學生的評價要求就不能一樣。當個別學生因能力問題不能及時完成學習任務時，也要根據學生的進度給予適當的肯定，以增加學生的自信。
