簡介
函子首先現身於代數拓撲學,其中拓撲空間的連續映射給出相應的代數對象(如基本群、同調群或上同調群)的代數同態。在當代數學中,函子被用來描述各種範疇間的關係。“函子”(英文: Functor)一詞借自美國哲學家魯道夫·卡爾納普的用語。卡爾納普使用“函子”這一詞和函式之間的相關來類比謂詞和性質之間的相關。對卡爾納普而言,不同於當代範疇論的用法,函子是個語言學的辭彙。對範疇論者來說,函子則是個特別類型的函式。
定義
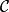 函子
函子 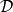 函子
函子 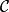 函子
函子 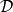 函子
函子 令和是兩個範疇。一個從到函子F由如下信息給出 :
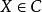 函子
函子 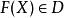 函子
函子 1)將每個對象映射至一對象上,
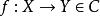 函子
函子 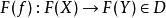 函子
函子 2)將每個態射映射至一態射上,使之滿足下列條件:
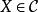 函子
函子 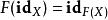 函子
函子 3)對任何對象,恆有。
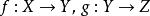 函子
函子 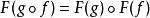 函子
函子 4)對任何態射,恆有。換言之,函子會保持單位態射與態射的複合。
一個由一範疇映射至其自身的函子稱之為“自函子”。
例子
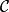 函子
函子 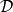 函子
函子  函子
函子 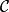 函子
函子  函子
函子 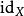 函子
函子 常函子(Constant functor):把中的所有對象都對應到中的一個固定的對象,且把中的態射都對應到的恆等態射。
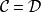 函子
函子 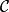 函子
函子 恆等函子(Identity functor):,把中的對象和態射都對應到其自身。
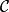 函子
函子 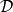 函子
函子 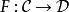 函子
函子 遺忘函子:“遺忘”掉某些結構的函子,例如是群全體和群同態構成的範疇,是集合全體和集合間的映射構成的範疇,則把群對應到去掉乘法運算後的集合,把群同態對應為映射就是一個遺忘函子。
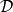 函子
函子 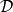 函子
函子 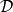 函子
函子 對角函子:對角函子被定義為由至函子範疇的函子,將每個在內的對象映射至此對象的常數函子上。
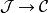 函子
函子 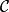 函子
函子 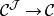 函子
函子 極限函子:對一固定的指標範疇,若每個函子都有個極限(即若為完全的),則極限函子即為將每個函子映射至其極限的函子。此類函子的存在性可以由將其理解為對角函子的右伴隨函子,且引入福端伴隨函子定理來證明之。這需要一個適當版本的選擇公理。相似的說法也可套用在上極限函子(其為協變的)之中。
雙函子與多函子
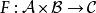 函子
函子 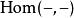 函子
函子 雙函子是函子概念在“雙變元”時的推廣。形式的定義則定義在兩個範疇的積上的函子。函子是一個自然的例子,它對第一個變元反變,對第二個變元協變。
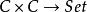 函子
函子 1) 雙函子是有“兩個”引數的函子。同態函子即為一個例子;其第一個引數為反變的,第二個引數則為協變的。形式上來說,雙函子是一個其定義域為積範疇的函子。例子,同態函子即為。
 函子
函子 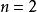 函子
函子 2) 多函子是將函子的概念廣義化至個引數。而雙函子當然是一個的多函子。
性質
從函子的公理中可得出兩個重要的推論 :
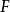 函子
函子 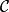 函子
函子 1)將每個在中的交換圖變換成中的一個交換圖;
 函子
函子 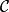 函子
函子 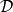 函子
函子 2) 若為中的一個同構,則 F( f)也會為中的一個同構。
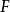 函子
函子 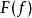 函子
函子  函子
函子 若函子滿足為同構若且唯若為同構,則稱之為 保守函子。
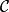 函子
函子 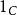 函子
函子  函子
函子 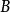 函子
函子  函子
函子 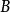 函子
函子 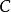 函子
函子  函子
函子 在任意範疇上,可定義一個單位函子,其將每個對象和態射映射至其自身。也可以將函子複合,即若 F為一由至的函子且為一由至的函子,則可組成一個由的複合函子。函子的複合依定義是可結合的。這顯示函子可以被認為是範疇的範疇中的態射。
一個只具單一對象的小範疇等同於一個么半群,此一單一對象範疇的態射可被視為是么半群中的元素,且其在範疇中的複合則可以視為是么半群中的運算。此時這類範疇間的函子無非是么半群間的同態。在此意義下,任意範疇間的函子可被視為是么半群同態至多於一個對象的範疇的一種廣義化。
具有特殊性質的函子
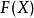 函子
函子 1) 本質滿射函子:使得值域中任意對象皆同構於某個的函子。
2) 正合函子:保存有限極限的函子。在阿貝爾範疇中相當於保存正合序列。
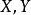 函子
函子 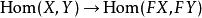 函子
函子 3) 忠實函子:使得對任意對象,為單射的函子。
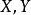 函子
函子 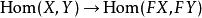 函子
函子 4) 完全函子:使得對任意對象,為滿射的函子。
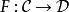 函子
函子 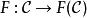 函子
函子 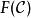 函子
函子 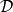 函子
函子 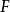 函子
函子 5) 完全忠實函子:既完全且忠實的函子稱為完全忠實函子。是完全忠實函子的充要條件是是範疇的等價,其中表示中由的像生成的滿子範疇。
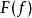 函子
函子  函子
函子 6) 保守函子:使得為同構若且唯若為同構的函子。
7) 加法函子:指預加法範疇(或加法範疇)中保存同態集(以及雙積)的阿貝爾群結構的函子。
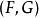 函子
函子 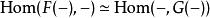 函子
函子 8) 伴隨函子:滿足下述條件時稱為一對伴隨函子:。
