伴隨函子

伴隨函子(對)(adjoint functor (pair))，亦稱相伴函子(對)。範疇論的基本概念之一。它在同調代數等學科中有著重要套用。該概念由坎(Kan, D.M.)於1958年提出。設F：L→D，G：D→L為兩個函子。若有自然等價h(—，—)：HomL(G(—),—)→HomD(—,F(—))，其中h(—，—)為集值二元映射（即，對∀ A∈L，B∈D，h(B,A)：HomL(G(B),A)→HomD(B,F(A))為雙射），則稱G為F的左伴隨函子，F為G的右伴隨函子，而(F,G)稱為伴隨函子(對)。例如，同調代數中的重要函子G=一ⓧB與F=Hom(B,—)為伴隨函子(對)。伴隨函子對有著重要的性質，例如，當(F,G)為伴隨函子對時，F必是右正合的，G必是左正合的。

簡介

在數學研究中，人們往往通過不同的方法來比較所研究的數學對象，例如在範疇論中，利用同構和等價來刻劃兩個研究對象是相同和等價的，然而同構和等價都是比較強的條件，伴隨函子是用更弱的條件來研究對象之間的關係。伴隨函子的概念最先是由坎(Kan, D.M.)於1958年提出來的，此後伴隨函子理論被廣泛套用於範疇、環與模論等研究領域，正如Saunders Mac Lane宣稱的那樣：伴隨函子無處不在，現在它已成為代數學的重要概念及工具之一。

伴隨函子等價定義

單位泛態射形式定義

給定兩個函子F：C→D與G:D→C，自然變換η:1→GF。F G稱為伴隨對，若對任意C∈C，D∈D，f:C→GD，存在惟一的g:FC→D，使得f=G(g)η。即

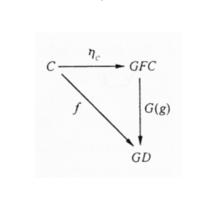伴隨函子

類似的，可以定義余單位泛態射來定義伴隨。

余單位泛態射形式定義

給定兩個函子F：C→D與G:D→C，自然變換δ:FG→1。F G稱為伴隨對，若對任意C∈C，D∈D，g:FC→D，存在惟一的f:C→GD，使得g=δF(f)。即

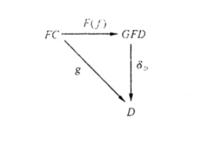伴隨函子

單位余單位形式定義

給定兩個函子F：C→D與G:D→C，兩個自然變換η:1→GF，δ:FG→1。F G稱為伴隨對，若對任意C∈C，D∈D，有下面的交換圖

伴隨函子

即δF·F=1F，Gδ·ηG=1。

Hom-Set形式定義

兩個函子F：C→D與G：D→C稱為伴隨對，若每對對象(C，D)，其中C∈C，D∈D，存在一個同構

ψ=ψ：D(FC,D)≅C(C,GD)。

注1：Hom(FC，D)常簡記為D(FC，D)=(FC，D)=(FC,D)。

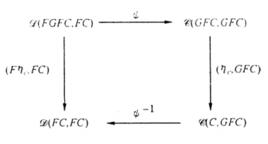
注2：ψ是雙射，且在C,D處是自然的，所以Hom(FC,D)事實上是一個雙函子，對所有的f:C″→C,g:D→D′，有下面兩個交換圖(*)

伴隨函子

伴隨函子的一個例子

伴隨函子在範疇論與表示論中有著廣泛套用，如單子余單子、Recollement等概念都是由伴隨函子給出的，下面是關於伴隨函子的一個重要例子。設B∈M，B⊗-是M到M張量函子，Hom(B,-)是M到MHom函子ψ:Hom(B⊗A,C)→Hom(A,Hom(B,C))是同構態射，並且對任意α∈Hom(A,A′)，γ∈Hom(A,A′)，有交換圖

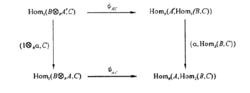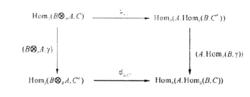伴隨函子

伴隨函子

因此，(B⊗-，Hom(B,-))是一對伴隨函子。