定義
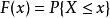 分布函式
分布函式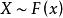 分布函式
分布函式設X是一個隨機變數,x是任意實數,函式 稱為X的分布函式。有時也記為 。
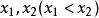 分布函式
分布函式對於任意實數 ,
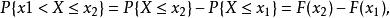 分布函式
分布函式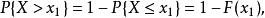 分布函式
分布函式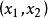 分布函式
分布函式因此,若已知X的分布函式,就可以知道X落在任一區間上的機率,在這個意義上說,分布函式完整地描述了隨機變數的統計規律性。
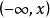 分布函式
分布函式如果將X看成是數軸上的隨機點的坐標,那么,分布函式F(x)在x處的函式值就表示X落在區間 上的機率。
分布函式的性質
F(x)為隨機變數X的分布函式,其充分必要條件為:
1.非降性
(1)F(x)是一個不減函式
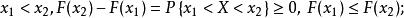 分布函式
分布函式對於任意實數
2.有界性
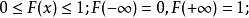 分布函式
分布函式(2)
 分布函式
分布函式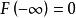 分布函式
分布函式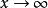 分布函式
分布函式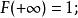 分布函式
分布函式從幾何上說明,將區間端點x沿數軸無限向左移動(即 ),則“隨機點X落在點x左邊”這一事件趨於不可能事件,從而其機率趨於0,即有 ;又若將點x無限右移(即 ),則“隨機點X落在點x左邊”這一事件趨於必然事件,從而趨於機率1,即有
3右連續性
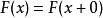 分布函式
分布函式(3) ;
證明:因為 F(x)是單調有界非減函式,所以其任一點x的右極限F(x+0)必存在。
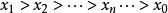 分布函式
分布函式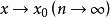 分布函式
分布函式為證明右連續,由海涅定理,只要對單調下降的數列 當 時,
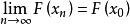 分布函式
分布函式證明 成立即可。 因為 :
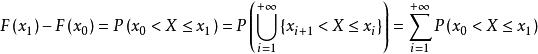 分布函式
分布函式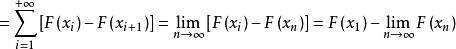 分布函式
分布函式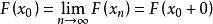 分布函式
分布函式所以得,
離散性隨機變數的分布函式
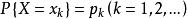 分布函式
分布函式設離散性隨機變數X的分布列為
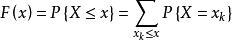 分布函式
分布函式由機率的可列可加性得 ,
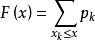 分布函式
分布函式即
 分布函式
分布函式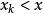 分布函式
分布函式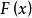 分布函式
分布函式 分布函式
分布函式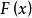 分布函式
分布函式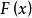 分布函式
分布函式 分布函式
分布函式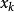 分布函式
分布函式 分布函式
分布函式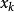 分布函式
分布函式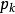 分布函式
分布函式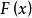 分布函式
分布函式 分布函式
分布函式其中和式是對滿足 的一切k求和.離散型隨機變數的分布函式是分段函式, 的間斷點就是離散型隨機變數的各可能取值點,並且在其間斷點處右連續.離散型隨機變數 的分布函式 的圖形是階梯形曲線. 在 的一切有(正)機率的點 ,皆有一個跳躍,其跳躍度正好為 取值 的機率 ,而在分布函式 的任何一個連續點x上, 取值x的機率皆為零。
離散型隨機變數的分布律和它的分布函式是相互唯一決定的。它們皆可以用來描述離散型隨機變數的統計規律性,但分布律比分布函式更直觀簡明,處理更方便。因此,一般是用分布律(機率函式)而不是分布函式來描述離散型隨機變數。
連續性隨機變數的分布函式
1.定義
 分布函式
分布函式設X為連續型隨機變數,其密度函式為 ,則有
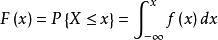 分布函式
分布函式對上式兩端求關於x的導數得
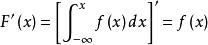 分布函式
分布函式這正是連續型隨機變數X的分布函式與密度函式之間的關係。
2.幾種常見的連續性隨機變數的分布函式
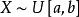 分布函式
分布函式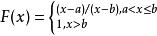 分布函式
分布函式(1)設 ,則隨機變數X的分布函式為
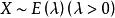 分布函式
分布函式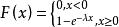 分布函式
分布函式(2)設 ,則隨機變數X的分布函式為
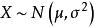 分布函式
分布函式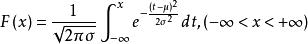 分布函式
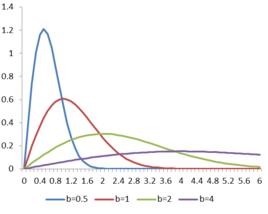
分布函式(3)設 ,則隨機變數的分布函式為
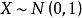 分布函式
分布函式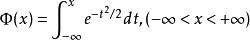 分布函式
分布函式對於 ,其分布函式為
聯合分布函式
定義
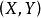 分布函式
分布函式給定一個隨機變數 ,稱定義域為整個平面的二元實值函式
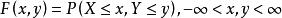 分布函式
分布函式為隨機變數(X,y)的分布函式。或稱為X與y的聯合分布函式.
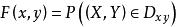 分布函式
分布函式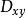 分布函式
分布函式按照分布函式的定義:,其中,區域 如右圖所示
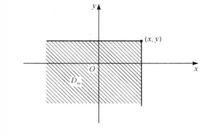 F(x,y)的幾何解釋
F(x,y)的幾何解釋性質
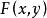 分布函式
分布函式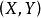 分布函式
分布函式設 是隨機變數 的分布函式,
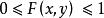 分布函式
分布函式(1) ;
(2)固定一個自變數的值時,作為一元函式關於另一個自變數是單調不減的;
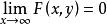 分布函式
分布函式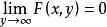 分布函式
分布函式(3)對任意固定一個y, ;對任意同固定一個x, ;
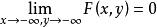 分布函式
分布函式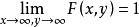 分布函式
分布函式(4) , ;
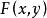 分布函式
分布函式(5)固定一個自變數的值時, 作為一元函式關於另一個自變數至少有連續;
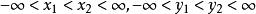 分布函式
分布函式(6)對任意的 有:
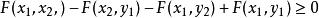 分布函式
分布函式。