重要參量
Fermi-Dirac分布函式的重要參量是費米能級。
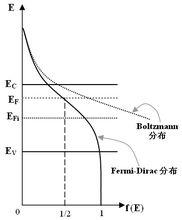F-D分布和Boltzmann分布費米能級的物理意義就表示能量為Ef的能級上的一個狀態被電子占據的幾率等於1/2。則：比費米能級高的狀態，未被電子占據的幾率大，即空出的狀態多（占據幾率近似為0）；相反，比費米能級低的狀態，被電子占據的幾率大，即可近似認為基本上被電子所占據（占據幾率近似為1）。
費米分布反映了Pauli不相容原理，故是一種 量子分布函式；即是簡併載流子必須遵從的統計分布函式。
當能量E比Ef大於3kT時，費米分布即退化為經典的 Boltzmann分布：f(E) ≈ exp[－(E－Ef)/kT]。對於摻雜濃度不是很高的非簡併半導體，載流子濃度不是很大，則載流子僅占據能帶極值附近的一些狀態，故往往滿足(E－Ef)>3kT條件，從而可以採用簡單的Boltzmann分布、而不必採用複雜的Fermi分布來進行討論。
由於費米能級不是一條真正的能級，所以它可以處在能帶的任何位置，即可以在禁帶中，也可以在能帶中。在本徵半導體或者絕緣體中，費米能級基本上是處在禁帶中央，這即意味著如果存在載流子的話，那么必定“電子濃度=空穴濃度”。在n型半導體中，因為導帶電子較多，則費米能級處在導帶底附近；在p型半導體中，因為價帶空穴較多，則費米能級處在價帶頂附近。假若費米能級進入到了導帶，即表明自由電子特別多，則為簡併的n型半導體；假若費米能級進入到了價帶，即表明自由空穴特別多，則為簡併的p型半導體。
適用條件
Fermi-Dirac分布函式或者Boltzmann分布函式是熱平衡狀態下的一種統計分布函式。因此Fermi-Dirac分布函式或者Boltzmann分布函式及其相應的費米能級等概念，也只能適用於熱平衡狀態，對於非平衡狀態則否。
在非平衡半導體中，非平衡載流子濃度的大小不能直接採用費米能級來表示，但是可以引入所謂 準費米能級來表示（即認為導帶電子系統和價帶空穴系統是分別處於 準熱平衡狀態）。這時系統中的電子準費米能級與空穴準費米能級之差，就反映了外界作用（譬如電壓）的大小。
