基本介紹
在複數範圍內,1的n(n∈N)個不同的n次方根都稱為 n次單位根,簡稱單位根。它們是
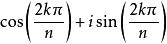 n次單位根
n次單位根 或
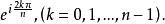 n次單位根
n次單位根 n次單位根是方程ω -1=0的n個不同的根,除ω=1外,其餘n-1個也是n-1次方程ω +ω +…+ω+1=0的n-1個不同根 。
n次單位根的性質
n次單位根有下列性質 :
1.對於任何m∈Z
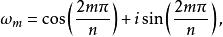 n次單位根
n次單位根 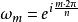 n次單位根
n次單位根 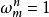 n次單位根
n次單位根 或都是n次單位根,即,但不同的單位根只有n個。例如取m=0,1,2,…,n-1時,就得到n個不同的n次單位根。當整數m=qn+k(q∈Z ,k∈{0,1,2,…,n-1})時,ω=ω=ω。
2.n次單位根的模為1,即|ω|=1。
3.兩個n次單位根ω,ω的乘積仍是一個n次單位根,且ω·ω=ω(i,j為任意整數)。由此可得:
1) (ω) =ω。
2) (ω) =ω(m,k為任意整數,當m=0時,(ω) =1=ω)。
3) ω=ω的充分必要條件是k與l除以n後餘數相同,即k與l的差是n的倍數。
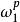 n次單位根
n次單位根 4) 任何一個單位根都可以寫成ω的冪,如ω=(ω) ,有這種性質的n次單位根ω稱為n次本原單位根,簡稱n次原根或原根,當p與n互素且1≤p
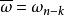 n次單位根
n次單位根 5) 一個n次單位根的共軛複數也是一個n次單位根,表示為。
6) 對任何整數k,l有(ω) =(ω) 。
4.設m是整數,則
 n次單位根
n次單位根 由此可知:
1) 全部單位根的和為0,即
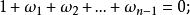 n次單位根
n次單位根 2) 設n次單位根ω≠1,則
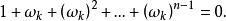 n次單位根
n次單位根 5.全部單位根把複平面上的單位圓周(|z|=1)n等分,構成了外接圓半徑為1的正n邊形的頂點,其中一個頂點是ω(1,0) 。