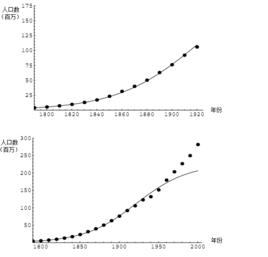
詳細介紹
與多重線性回歸的比較
logistic回歸(Logistic regression) 與多重線性回歸實際上有很多相同之處，最大的區別就在於他們的因變數不同，其他的基本都差不多，正是因為如此，這兩種回歸可以歸於同一個家族，即廣義線性模型（generalized linear model）。這一家族中的模型形式基本上都差不多，不同的就是因變數不同，如果是連續的，就是多重線性回歸，如果是二項分布，就是logistic回歸，如果是poisson分布，就是poisson回歸，如果是負二項分布，就是負二項回歸，等等。只要注意區分它們的因變數就可以了。
logistic回歸的因變數可以是二分非線性差分方程類的，也可以是多分類的，但是二分類的更為常用，也更加容易解釋。所以實際中最為常用的就是二分類的logistic回歸。
用途
一、尋找危險因素，正如上面所說的尋找某一疾病的危險因素等。
二、預測，如果已經建立了logistic回歸模型，則可以根據模型，預測在不同的自變數情況下，發生某病或某種情況的機率有多大。
三、判別，實際上跟預測有些類似，也是根據logistic模型，判斷某人屬於某病或屬於某種情況的機率有多大，也就是看一下這個人有多大的可能性是屬於某病。
這是logistic回歸最常用的三個用途，實際中的logistic回歸用途是極為廣泛的，logistic回歸幾乎已經成了流行病學和醫學中最常用的分析方法，因為它與多重線性回歸相比有很多的優勢，這些優勢將在以後的文章中一一介紹。本篇文章主要是先讓大家對logistic回歸有一個初步的了解，以後會對該方法進行詳細的闡述。
系統研究
一維和二維Logistic系統
生態學中的蟲口模型(亦即Logistic映射)可用來描述
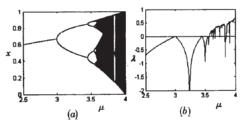Logistic模型x(n+1)=u*x(n)*(1-x(n)),u屬於[0,4],n屬於(0,1)這是1976年數學生態學家R. May在英國的《自然》雜誌上發表的一篇後來影響甚廣的綜述中所提出的，最早的一個由倍周期分岔通向混沌的一個例子。後來經過Feigenbaum研究得出:一個系統一旦發生倍周期分岔，必然導致混沌。他還發現並確定了該系統由信周期分岔通向混沌的兩個普適常數(也稱為Feigenbaum常數)。
對於一維Logistic映射，研究的比較早也比較詳細，比如該映射之所以產生混沌，有人歸納出它具有兩個基本性質、逆瀑布、周期3視窗、U序列等等。但是一維Logistic映射僅有一個自由度，利用它只能產生一條線或一條曲線，而做圖像，至少需要兩個或以上個自由度，為此，孫海堅等人給出了LMGS定義。王興元還擴展了LMGS定義，在此基礎上，就可以分析2維及其以上的系統，分析圖形與吸引子的結構特徵，探討了圖形與吸引子之間的聯繫;並由一維可觀察計算系統混沌定量判據的方法，計算了吸引子的Lyapunov指數和Lyaounov維數。
二維Logistic映射起著從一維到高維的銜接作用，對二維映射中混沌現象的研究有助於認識和預測更複雜的高維動力系統的性態。王興元教授通過構造一次藕合和二次藕合的二維Logistic映射研究了二維Logistic映射通向混沌的道路，分析了其分形結構和吸引盆的性質，指出選擇不同的控制參數，二維映射可分別按Feigenbaum途徑等走向混沌，並且指出在控制參數空間中的較大的區域，其通向混沌的道路與Hopf分岔有關，在這些途徑上可觀察到鎖相和準周期運動。二維滯後Logistic映射
x(n+1)=y(n)
y(N+1)=u*y(n)*(1-x(n)), u屬於(0,2.28),[x,y]屬於(0,1)
該系統走向混沌的道路正是驗證了二維Logistic映射與Neimark-Sacker分岔有密切的關係，對於研究其他的具有滯後的系統具有重要的意義。
軟體實現方式
在stata中，logistic回歸可以得到很好的實現。主要命令為：
其中，logistic為主命令，hcv為因變數，後面的三個變數依次為自變數。
如果自變數既存在啞變數又存在連續變數，系統自帶的help裡面沒有提到，可用如下方式：
其中，xi表示後面帶i.的變數將自動變為啞變數。
分岔圖（MATLAB實現）
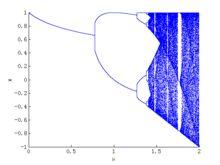Logistic模型蟲口模型分岔圖
