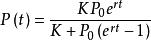Logistic函式
Logistic函式logistic函式其實就是這樣一個函式：，其中為初始值，K為終值，r衡量曲線變化快慢。
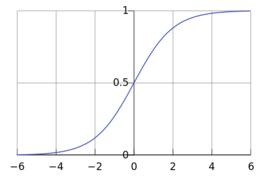
非常簡單吧，這個函式的曲線如下所示：
很像一個“S”型吧，所以又叫 sigmoid曲線（S型曲線）。
邏輯斯諦方程即微分方程：
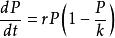Logistic函式當一個物種遷入到一個新生態系統中後，其數量會發生變化。假設該物種的起始數量小於環境的最大容納量，則數量會增長。該物種在此生態系統中有天敵、食物、空間等資源也不足（非理想環境），則增長函式滿足邏輯斯諦方程，圖像呈S形，此方程是描述在資源有限的條件下種群增長規律的一個最佳數學模型。在以下內容中將具體介紹邏輯斯諦方程的原理、生態學意義及其套用。
這還要追溯到1838年，一個比利時的數學家叫Pierre-François Verhulst（1804-1849）的人，他那個時候研究人口增長的課題，提出了人口增長不但和現有人口相關，還和可用資源有關，即有一個人口的承載量，首先將營養關係反映到種群數學模型方面，是它首先導出了後來被廣泛稱為邏輯斯諦的方程，最初發表的時候叫Verhulst方程。但在當時並沒有引起大家的注意，直到1920年兩位美國人口學家Pearl和Reed在研究美國人口問題時，再次提出這個方程，才開始流行，故現在文獻中通常稱之為Verhulst-Pearl阻礙方程。其所以又稱為邏輯斯諦方程是因為其有某種邏輯推理的含義。按現在的用語來說，它是一個說理模型，實際上是反映營養對種群增長的一種線性限制關係的說理模型。
1963年，洛倫茲發現確定性系統的隨機行為，並且發現了這種隨機行為對初值的敏感性。1975年，美籍華人學者李天岩和數學家約克發表“周期中蘊含著混沌”的著名文章，揭示從有序到混沌的演化過程。這些內容都包含在邏輯斯諦差分方程中。1976年R.梅在英國《自然》雜誌上發表了研究邏輯斯諦方程的成果—《表現非常複雜的動力學的簡單數學模型》，引起學術界極大關注，內容已遠遠超越了生態學領域，揭示出邏輯斯諦方程深處蘊藏的豐富內涵。
將上面的方程解出來，可以得到：
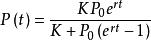Logistic函式 Logistic函式其中為初始值，很眼熟吧，變變形，是不是就類似開頭提出的logistic函式了，唯一不同的是係數有所變化。
