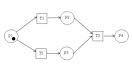
簡介
由於Petri網能夠表達並發的事件，被認為是自動化理論的一種。研究領域趨向認為Petri網是所有流程定義語言之母。
背景
卡爾·A·佩特里是一名物理學家，他發明Petri網主要是從物理的角度去描述並發現象的。據佩特里本人所述，他認為60年代自動機理論由於缺乏並發(Concurrence)概念不適合於表達現代物理學理論，例如狹義相對論(Special Relativity)和不確定性原理(Uncertainty Principle)。Petri網的一個重要的貢獻，就是Petri網裡面不存在所謂的“全局時間”的概念，它能夠很容易地表達狹義相對論的觀點。即Petri網可以描述每一個節點的擁有自己的獨立時序，只要條件滿足，就可以發生。
從狹義相對論的觀點出發，兩個時空點之間如果沒有因果關係把它們連線起來（或者說“類空”的），它們就是獨立的，不能說其中一個發生在前另一個在後或者相反。因此，Petri網裡面的兩種變遷（見下文）如果都有發生的條件，則不能認為其執行順序有任何關係。然而，Petri網旨在描述變遷之間的因果關係，並由此構造時序。
經典模型
經典的Petri網是簡單的過程模型，由兩種節點：庫所和變遷，有向弧，以及令牌等元素組成的。
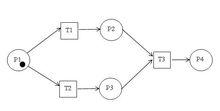Petri網結構
(1) Petri網的元素：
+ 庫所（Place）圓形節點
+ 變遷（Transition）方形節點
+ 有向弧（Connection）是庫所和變遷之間的有向弧
+ 令牌（Token）是庫所中的動態對象，可以從一個庫所移動到另一個庫所。
規則
+ 有向弧是有方向的
+ 兩個庫所或變遷之間不允許有弧
+ 庫所可以擁有任意數量的令牌
o 行為
如果一個變遷的每個輸入庫所（input place）都擁有令牌，該變遷即為被允許(enable)。一個變遷被允許時，變遷將發生(fire)，輸入庫所(input place)的令牌被消耗，同時為輸出庫所(output place)產生令牌。
+ 變遷的發生是完整的，也就是說，沒有一個變遷只發生了一半的可能性。
+ 有兩個或多個變遷都被允許的可能，但是一次只能發生一個變遷。這種情況下變遷發生的順序沒有定義。
+ 如果出現一個變遷，其輸入庫所的個數與輸出庫所的個數不相等，令牌的個數將發生變化，也就是說，令牌數目不守恆。
+Petri網路是靜態的，也就是說，不存在發生了一個變遷之後忽然冒出另一個變遷或者庫所，從而改變Petri網結構的可能。
+ Petri網的狀態由令牌在庫所的分布決定。也就是說，變遷發生完畢、下一個變遷等待發生的時候才有確定的狀態，正在發生變遷的時候是沒有一個確定的狀態的。
兩個變遷爭奪一個令牌的情形被稱之為衝突。當發生衝突的時候，由於Petri網的時序是不確定的，因此具體哪個變遷得以發生也是不確定的。實際套用中，往往需要避免這種情形。用於描述現象的Petri網也可能自然出現衝突，這表明我們對於變遷發生的條件沒有完全了解。
多個弧連線兩個節點的情況。在輸入庫所和變遷之間的弧的個數決定了該變遷變為被允許需要的令牌的個數。弧的個數決定了消耗/產生的令牌的個數。
定義
一個經典的Petri網由四元組（庫所，變遷，輸入函式，輸出函式）組成。任何圖都可以映射到這樣一個四元組上，反之亦然。
被允許的形式化 變遷發生的形式化 Petri網到變遷系統的映射 可達性圖
Petri 是一個三元組(P,T,F)， F(P X T)U(T X P)是弧的集合
流程
一個流程的狀態是由在場所中的令牌建模的，狀態的變遷是由變遷建模的。令牌表示事物（人，貨物，機器），信息，條件，或對象的狀態； 庫所代表庫所，通道或地理位置；變遷代表事件，轉化或傳輸。
一個流程有當前狀態，可達狀態，不可達狀態。終止狀態。
局限
+ 沒有測試庫所中零令牌的能力
+ 模型容易變得很龐大
+ 模型不能反映時間方面的內容
+ 不支持構造大規模模型，如自頂向下或自底向上
高級模型
為了解決經典Petri網中的問題，研究出了高級Petri網，在以下方面進行了擴展：
o 令牌著色
一個令牌通常代表具有各種屬性的對象，因此令牌擁有值（顏色）代表由令牌建模的對象的具體特徵，如一個令牌代表一個工人（張三，28歲，經驗3級）。
o 時間
為了進行分析，我們需要建模期間，延遲等，因此每一個令牌擁有一個時間戳，變遷決定生產出的令牌的延遲。
o 層次化
構造一個複雜性與數據流圖相當的Petri網的機制。子網是由庫所，變遷和子網構成的網路。
o 時序
增加時序邏輯的定義，更好的描述行為過程。
套用
Petri網的套用非常廣泛，以下是Petri網比較常用的幾種套用：
o 軟體設計
o工作流管理
o 工作流模式
o 數據分析 故障診斷
o 並行程式設計
o 協定驗證
