PID控制算法(ProportionalIntegral-Differential,比例一積分一微分)作為一種最常規,最經典的控制算法,經過了長期的實踐檢驗。因為這種控制具有簡單的結構,對模型誤差具有魯棒性及易於操作等優點,在實際套用中又較易於整定,所以它在工業過程控制中有著廣泛的套用 。有調查表明,在煉油、化工、造紙等過程超過11,000個控制器中,有超過9796的控制器是PID類控制器 ,PID控制器在嵌入式系統中的套用也在增長[6]。
PID整定方法
Z - N參數整定法
Ziegler-Nichol回響曲線法 ,是根據被控對象的階躍回響曲線獲取被控對象的模型式(1),根據模型的增益K,時間常數T以及純滯後時間,再利用如下的經驗公式(2)整定PID控制器參數。
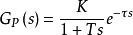 PID整定
PID整定公式(1):
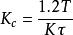 PID整定
PID整定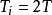 PID整定
PID整定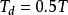 PID整定
PID整定公式(2): , ,
一般來說由於Z-N整定的PID控制器超調較大。為此C.C.Hang提出改進的Z-N法[8],通過給定值加權和修正積分常數改善了系統的超調。這種方法被認為是Z-N法最成功的改進。
Ziegler-Nichols臨界振盪法只對開環穩定對象適用。該方法首先對被控對象施加一個比例控制器,並且其增益很小,然後逐漸增大增益使系統出現穩定振盪·則此時臨界振盪增益就是比例控制器的數值K,,振盪周期就是系統的振盪周期凡,然後根據公式(3)整定PID控制器參數。
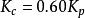 PID整定
PID整定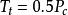 PID整定
PID整定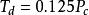 PID整定
PID整定公式(3): , ,
類似的整定方法有Cohen-Coon回響曲線方法[9],該方法同Ziegler-Nichols回響曲線法操作相同,只是整定公式不同,其整定公式如式(4):
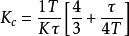 PID整定
PID整定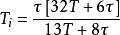 PID整定
PID整定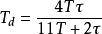 PID整定
PID整定公式(4): , ,
基於誤差性能指標的整定方法
為評價控制性能的優劣,定義了多種積分性能指標,基於誤差性能指標的參數整定方法 是以控制系統瞬時誤差函式e(θ,t)的泛函積分評價Jn(θ)為最優控制指標,它是評價控制系統性能的一類標準,是系統動態特性的一種綜合性能指標,一般以誤差函式的積分形式表示。其中Jn(θ)的基本形式如式(5):
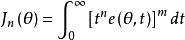 PID整定
PID整定公式(5):
n=0,m=0IAE
n=0,m=2ISE
n=1,m=2ISTE
Jn(θ)可以是ISE,1AE,1STE,1TAE等,然後經過尋優,搜尋出一組PID控制器參數Kc,Ti,Td,使Jn(θ)的取值為最小,此時的PID控制器參數為最優。
內模(IMC;Internal Model Control))整定
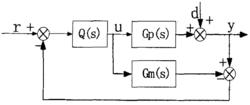
根據內模控制系統 , 與常規反饋控制系統間存在的對應關係,必要時對模型進行降階簡化處理,便可完成IMC-PID設計 內模控制系統結構如下圖所示。
 PID整定
PID整定圖中Gp(s)為實際被控過程對象,Gm(s)為被控過程的數學模型,即內部模型,Q(s)為內模控制器,它等於Gm(s)的最小相位部分的逆模型。u為內模控制器的輸出,r,y,d分別為控制系統的輸入、輸出和干擾信號。
為抑制模型誤差對系統的影響,增強系統的魯棒性,在控制器中加人一個低通濾波器F(s),一般F(s)取最簡單形式如下:
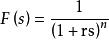 PID整定
PID整定公式(6):
式中階次n取決於模型的階次以使控制器可實現,r為時間常數。則內模控制等效的控制器為:
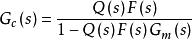 PID整定
PID整定公式(7):
對於如式(1)表示的一階加純滯後過程,採用一階Pade近似,得到如下模型:
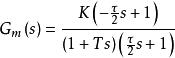 PID整定
PID整定公式(8):
將式(8)的最小相位部分代入式(7),可得到如下的PID控制器參數:
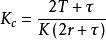 PID整定
PID整定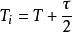 PID整定
PID整定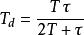 PID整定
PID整定公式(9):,,
