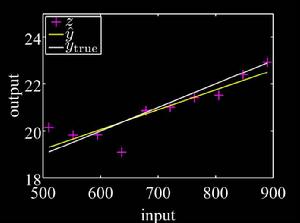
定義
L1範數（L1 norm）是指向量中各個元素絕對值之和，也有個美稱叫“稀疏規則運算元”（Lasso regularization）。
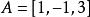L1範數正則化
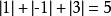L1範數正則化比如 向量 ， 那么A的L1範數為
原理
在支持向量機（support vector machine）學習過程中，實際是一種對於成本函式(cost function)求解最優的過程。
成本函式的構建原理
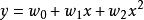L1範數正則化例如我們有一個數學模型的樣子(structure)， ，其中x是輸入，y是輸出。
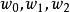L1範數正則化如果我們已知 ，那么我們可以根據任何輸入x的值，知道輸出y的值。這叫預測(prediction)。
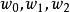L1範數正則化 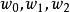L1範數正則化因此，問題進化為，我們手裡有很對很多組x對應的y，但是不知道 ！我們想通過測量很多組的x和y，來推斷出 為多少。
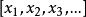L1範數正則化
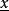L1範數正則化
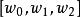L1範數正則化
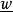L1範數正則化我們將 T記為 ， 記為 。
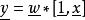L1範數正則化那么原式則寫為
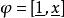L1範數正則化若
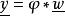L1範數正則化那么
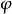L1範數正則化
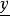L1範數正則化 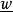L1範數正則化因此我們現在知道 和 ，我們希望通過計算得到 ！
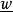L1範數正則化 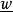L1範數正則化由於我們手中的很多組x和y都是通過實驗的結果測試出來的。測量的結果就會有誤差，因此 不可能計算的精準，那么我們很容易想到使用最小二乘法(least square) 來計算 。
我們構建一個方程，這個方程也是最小二乘法的核心
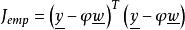L1範數正則化 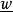L1範數正則化
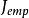L1範數正則化線性回歸的本質，就是找到一組 ， 能夠讓 最小！
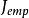L1範數正則化因此，就是我們的成本函式。
用最小二乘法學習的問題
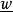L1範數正則化如果我們的問題是’灰箱‘（grey box）（即我們已經知道數學模型，而不知道參數），直接用最小二乘法找到 是很簡潔的。
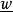L1範數正則化如果我們的問題是‘黑箱’（black box） （即 我們既不知道數學模型，也不知道參數），在擬合時，我們就不知道我們需要用幾階的多項式模型來逼近（或者幾個核函式來逼近（kernel function），為了簡便，不在這裡贅述）。那么我們甚至連 的個數都不知道。
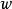L1範數正則化我們只能通過嘗試和專家經驗來猜測階數。如果我們的階數猜測多了，就會多出很多冗餘的項。我們希望這些冗餘項對應的權值 為0，這樣我們就知道哪些項是無關的，是冗餘的項。
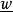L1範數正則化 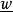L1範數正則化但是只用最小二乘法確定 時，可能所有的 的絕對值都極其巨大，這是很正常的現象，但是它使得我們無法剔除無關項，得到的模型也毫無實際意義，模型處於ill-condition狀態 (即輸入很小的變化，就會引起輸出病態的巨大的變化)。
最大複雜度模型+L1正規化（懲罰項）
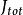L1範數正則化我們在成本函式中加入L1範數（其實就是懲罰項），成本函式 變為
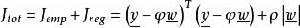L1範數正則化
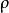L1範數正則化其中 是我們用來控制L1正規化影響的權重係數。
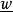L1範數正則化 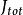L1範數正則化因此，我們的目標成為了 ： 找到一組 使得 最小！
繼而使用最小二乘法，完成運算。
為什麼要這樣構建成本函式？？？
如上文所述，監督機器學習問題無非就是“minimize your error while regularizing your parameters”，也就是在規則化參數的同時 最小化誤差（最小二乘法的原理）。最小化誤差是為了讓我們的模型擬合我們的訓練數據，而規則化參數是防止我們的模型過分擬合我們的訓練數據。因為參數太多，會導致我們的模型複雜度上升，容易過擬合，也就是我們的訓練誤差會很小。但訓練誤差小並不是我們的最終目標，我們的目標是希望模型的測試誤差小，也就是能準確的預測新的樣本。所以，我們需要保證模型“簡單”的基礎上 最小化訓練誤差，這樣得到的參數才具有好的泛化性能（也就是測試誤差也小），而模型“簡單”就是通過規則函式來實現的。另外，規則項的使用還可以約束我們的模型的特性。這樣就可以將人對這個模型的先驗知識融入到模型的學習當中，強行地讓學習到的模型具有人想要的特性，例如稀疏、低秩、平滑等等。
