在數學中
數學性質
•第31個素數。前一個為113、下一個為131。
•100以上第6個質數
•第4個梅森素數(2⁷-1):對應完全數為 8128,8128=64×127=2⁶×(2⁷-1)。前一個為31、下一個為8191。
•第10個幸運素數
•第4個梅森質數及第3個雙重梅森數
•2¹²⁷-1亦是梅森質數,盧卡斯在1876年發現。他聲稱用了19年時間以雙手算出這個結果。
•高斯質數之一。
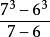 127
127●立方質數:
•第96個虧數,真約數和為1,虧度為126。前一個為125、下一個為128。
•第87個不尋常數,大於平方根的素因數為127。前一個為124、下一個為129。
•第78個無平方數因數的數。前一個為123、下一個為129。
•第54個十進制的等數位數。前一個為123、下一個為129。
•第7箇中心六邊形數
•第7個默慈金數
•127 在二進制中是循環單位(1111111)。
•127可以變成算式-1+2⁷=-1+128=127,結果正好等於127本身。
•第26個質數+26(101+26)=127。
•第4個梅森質數,簡稱M4
•第7個梅森數,簡稱P7
趣味數學
•十進制中的傅利曼數 :,而且組成數字在算式出現順序和數字本身順序一致,所以是好傅利曼數;二進制中也是:127=-1+2⁷
•1234567的最小質因子
•最小的數(大於5)不能表示成2的乘方和一質數的和
•127²×31+1=500000
•1/127=0.007874015748031496062992125984251968503937(倒數循環節42位,後六位是前六位的兩倍,最後六位是其前六位兩倍加1)
純質數
127是第31個質數
31是第11個質數
11是第5個質數
5是第3個質數
3是第2個質數
2是第1個質數
從頭到尾,直到變成1,都沒有出現合數,所以我們可以說127是一個“純質數”。 如果把1也定義成“純質數”的話(雖然1本身不是質數),那么127正好是第 7個“純質數”,與127=2 ⁷-1恰好相吻合。第6個“純質數”31正好也是2 -1型的數,不過它的n=5。
倍數表
| 乘數 | 乘積 |
| 1 | 127 |
| 2 | 254 |
| 3 | 381 |
| 4 | 508 |
| 5 | 635 |
| 6 | 762 |
| 7 | 889 |
| 8 | 1,016 |
| 9 | 1,143 |
| 10 | 1,270 |
| 11 | 1,397 |
| 12 | 1,524 |
| 13 | 1,651 |
| 14 | 1,778 |
| 15 | 1,905 |
| 16 | 2,032 |
| 17 | 2,159 |
| 18 | 2,286 |
| 19 | 2,413 |
| 20 | 2,540 |
| 21 | 2,667 |
| 22 | 2,794 |
| 23 | 2,921 |
| 24 | 3,048 |
| 25 | 3,175 |
| 26 | 3,302 |
| 27 | 3,429 |
| 28 | 3,556 |
| 29 | 3,683 |
| 30 | 3,810 |
| 31 | 3,937 |
| 32 | 4,064 |
| …… | |
在人類文化中
將2×31×127²乘起來,就是999998。
將127×9721=1234567
1+126=127
有人認為,127是第七個梅森素數 ,簡稱M7,實際上它是第四個梅森素數,是M4,是第七個梅森數,是P7。
上世紀90年代至本世紀初,127是自動尋呼台的號碼。撥127+尋呼機號,便可在該尋呼機上顯示撥打時所用的電話號碼。
在其他領域中
•公元127年(127年)
•公元前127年
•1月27日
•12月7日
•刪除的ASCII和Unicode碼。
•ASCII字元有0至127。
•8位元二補數所能表示的最大正整數。
•《127小時》,美國電影
•這部電影講述了一位美國登山青年如何斷臂求生的故事。

