基本介紹
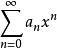 麥克勞林級數
麥克勞林級數對於一個給定的函式f(x),如果能找到一個冪級數 ,使
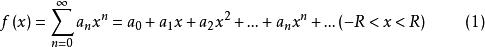 麥克勞林級數
麥克勞林級數成立,則稱f(x) 可展開成x的冪級數。但要將f(x)展開成x的一個冪級數,需解決兩個以下問題:
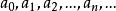 麥克勞林級數
麥克勞林級數(1)如何確定式(1)中的係數 ?
(2)按所求得的係數,這個冪級數在它的收斂域內的和函式是否就是f(x)?
先解決問題(1),不妨設式(1)成立。那么。根據冪級數可以逐項求導的性質,依次求出式(1)中的各階導數:
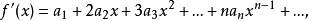 麥克勞林級數
麥克勞林級數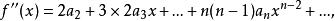 麥克勞林級數
麥克勞林級數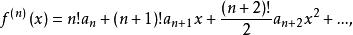 麥克勞林級數
麥克勞林級數把x=0代人式(1)及上述各式,得
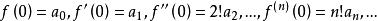 麥克勞林級數
麥克勞林級數於是
 麥克勞林級數
麥克勞林級數把它們代回式(1),得
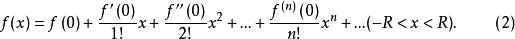 麥克勞林級數
麥克勞林級數通常稱式(2)為f(x)的 麥克勞林展開式或f(x)在x=0處的 冪級數展開式。式(2)中等號右端的級數稱為f(x)的 麥克勞林級數或f(x)展開成x的冪級數。
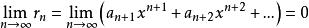 麥克勞林級數
麥克勞林級數至於問題(2)。只要證明其餘項滿足即可(證明略)。
下面考慮在什麼條件下,函式f(x)能展開成麥克勞林級數。
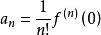 麥克勞林級數
麥克勞林級數可見,按公式求得係數的冪級數在它的收斂域內的和函式就是f(x) 。
麥克勞林級數展開的條件及方法
定理1設函式f(x)的麥克勞林級數的收斂半徑R>0,當n→∞時,如果函式f(x)在任一固定點x處的n階導數f (x)有界,則函式f(x)在收斂區間(-R,R)內能展開成麥克勞林級數 。即
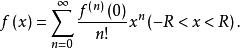 麥克勞林級數
麥克勞林級數把函式f(x)展開成冪級數,有 直接展開法和 間接展開法 。
直接展開法
利用麥克勞林級數公式將函式f(x)展開成x的冪級數的方法,稱為 直接展開法。步驟可歸納為:
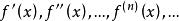 麥克勞林級數
麥克勞林級數 麥克勞林級數
麥克勞林級數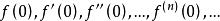 麥克勞林級數
麥克勞林級數(1)求出f(x)的各階導數,令得
(2)寫出f(x)的麥克勞林級數
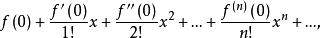 麥克勞林級數
麥克勞林級數並求出收斂半徑R。
間接展開法
利用麥克勞林級數展開函式,需要求高階導數,比較麻煩,如果能利用已知函式的展開式,根據冪級數在收斂域內的性質,將所給的函式展開成冪級數,這種方法稱為間接展開法 。

